3 10 As A Percentage
defexpoindia
Sep 22, 2025 · 5 min read
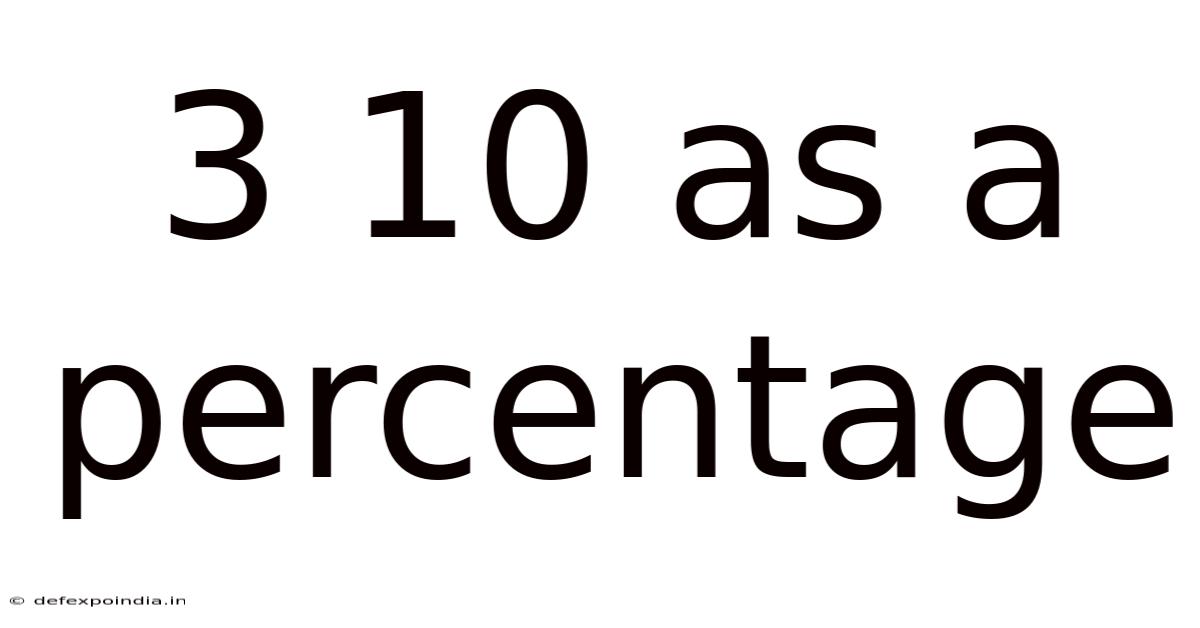
Table of Contents
Understanding 3/10 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics, frequently applied in various real-world scenarios from calculating grades to understanding financial data. This article will delve deep into understanding how to convert the fraction 3/10 into a percentage, exploring the underlying principles, providing step-by-step instructions, and addressing common questions. We'll also explore the broader context of fraction-to-percentage conversions and their practical applications.
What is a Percentage?
Before we tackle the conversion of 3/10, let's clarify the concept of a percentage. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" – the symbol "%" represents this. For instance, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Percentages are widely used to represent proportions, rates, and changes in various contexts.
Converting Fractions to Percentages: The Fundamental Principle
The core principle behind converting a fraction to a percentage involves two key steps:
- Convert the fraction to a decimal: To do this, divide the numerator (the top number) by the denominator (the bottom number).
- Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
Let's apply this to various examples before tackling 3/10 specifically.
Example 1: Converting 1/2 to a percentage
- Decimal Conversion: 1 ÷ 2 = 0.5
- Percentage Conversion: 0.5 × 100 = 50%
Example 2: Converting 3/4 to a percentage
- Decimal Conversion: 3 ÷ 4 = 0.75
- Percentage Conversion: 0.75 × 100 = 75%
Example 3: Converting 7/8 to a percentage
- Decimal Conversion: 7 ÷ 8 = 0.875
- Percentage Conversion: 0.875 × 100 = 87.5%
Converting 3/10 to a Percentage: A Step-by-Step Guide
Now, let's apply this method to the fraction 3/10:
- Decimal Conversion: 3 ÷ 10 = 0.3
- Percentage Conversion: 0.3 × 100 = 30%
Therefore, 3/10 is equivalent to 30%.
Visual Representation of 3/10 as a Percentage
Visual aids can enhance understanding. Imagine a pie chart divided into 10 equal slices. If 3 of these slices are shaded, representing the fraction 3/10, then the shaded portion represents 30% of the whole pie. This visual representation solidifies the concept of 3/10 as 30%. Similarly, a bar graph with 10 equal sections, where 3 are filled, would also visually demonstrate the 30% representation.
Understanding the Relationship Between Fractions, Decimals, and Percentages
It's crucial to understand the interconnectedness of these three mathematical representations. They are simply different ways of expressing the same proportion or quantity. You can freely convert between them using the methods outlined above. The ability to seamlessly move between fractions, decimals, and percentages is essential for effective problem-solving in many areas.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is not just a theoretical mathematical exercise; it finds extensive real-world applications:
- Calculating Grades: If you answer 3 out of 10 questions correctly on a test (3/10), your score is 30%.
- Financial Calculations: Understanding percentages is essential for calculating interest rates, discounts, taxes, profit margins, and more. For example, a 30% discount on a product is easily calculated once you understand the percentage concept.
- Data Analysis: Percentages are used extensively to represent data in charts and graphs, making it easier to visualize and understand trends and patterns.
- Probability and Statistics: Percentages are used to express probabilities and statistical measures, helping us understand the likelihood of events.
- Everyday Life: From calculating tips in restaurants to understanding sales tax, percentages are ingrained in our daily lives.
Advanced Concepts and Further Exploration
While this article focuses on the simple conversion of 3/10, let's briefly touch upon more complex scenarios:
- Converting fractions with larger denominators: The same principles apply, even if the denominator is not a factor of 100. You would simply divide the numerator by the denominator and multiply by 100.
- Converting mixed numbers: A mixed number (e.g., 1 1/2) needs to be converted to an improper fraction before applying the conversion process.
- Percentages greater than 100%: These represent proportions larger than the whole, often used to denote growth or increase.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to convert fractions to percentages?
A1: Converting fractions to percentages is a fundamental skill that helps us understand and interpret proportions in various contexts, from academic assessments to financial decisions and data analysis.
Q2: Can I convert a percentage back to a fraction?
A2: Yes, absolutely. To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 30% becomes 30/100, which simplifies to 3/10.
Q3: Are there any online calculators to help with fraction-to-percentage conversions?
A3: While this article provides the manual methods, many online calculators are readily available to assist with fraction-to-percentage conversions and other mathematical operations.
Q4: What if the decimal resulting from the fraction division is a long repeating decimal?
A4: In such cases, you would round the decimal to a suitable number of decimal places before multiplying by 100. The level of precision required will depend on the context of the problem.
Conclusion
Converting 3/10 to a percentage is a straightforward process that involves converting the fraction to a decimal and then multiplying by 100. The resulting percentage, 30%, represents a proportion, allowing for easy comparison and interpretation in various applications. Understanding this fundamental conversion is essential for anyone navigating the world of mathematics, finance, and data analysis. Remember the interconnectedness of fractions, decimals, and percentages, and use the appropriate representation based on the context. This fundamental skill will serve you well in many aspects of life.
Latest Posts
Latest Posts
-
67 Fahrenheit Convert To Celsius
Sep 22, 2025
-
Whats 100 Cm In Inches
Sep 22, 2025
-
Calculadora De Kilogramos A Libras
Sep 22, 2025
-
1 4 Mm To Mm
Sep 22, 2025
-
2 75 Inches On A Ruler
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3 10 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.