Whats 20 Percent Of 14
defexpoindia
Sep 20, 2025 · 5 min read
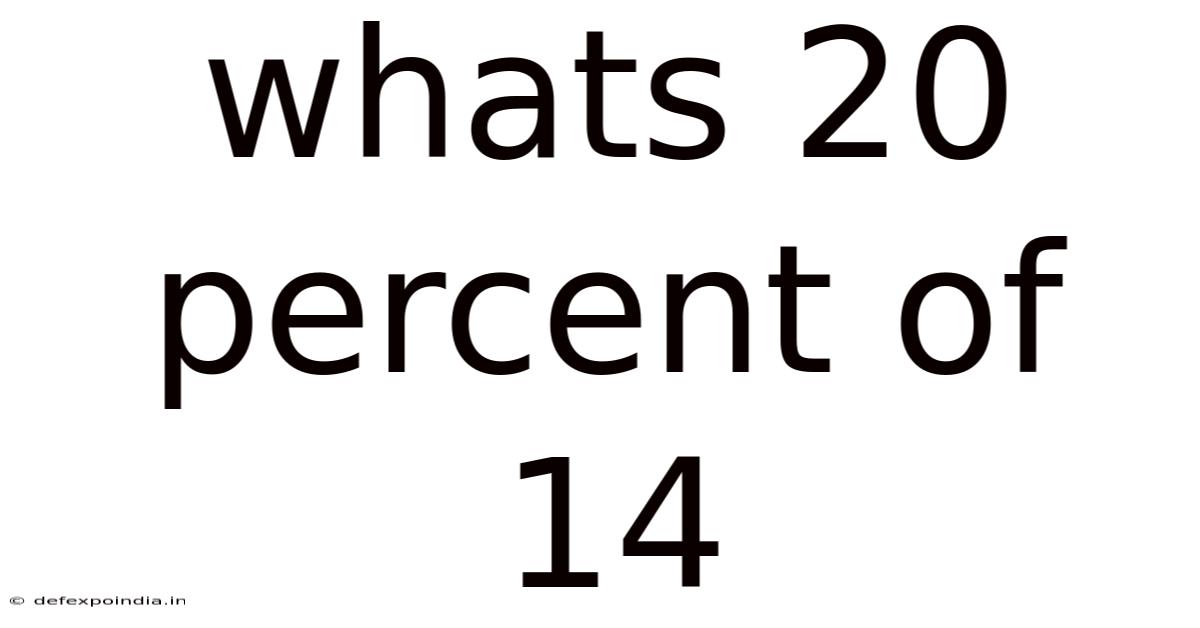
Table of Contents
What's 20 Percent of 14? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 14 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This seemingly straightforward question allows us to explore various methods of calculation, delve into the practical applications of percentages in everyday life, and even touch upon some advanced mathematical concepts. This article will not only answer the question "What's 20 percent of 14?" but also equip you with the knowledge and skills to tackle similar problems with confidence.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). So, 20 percent (20%) means 20 out of 100, or 20/100, which simplifies to 1/5. Understanding this fundamental concept is key to solving percentage problems.
Method 1: Using the Formula
The most straightforward method to calculate a percentage of a number involves using a simple formula:
(Percentage/100) * Number = Result
In our case:
(20/100) * 14 = 2.8
Therefore, 20 percent of 14 is 2.8.
Method 2: Decimal Conversion
Another effective approach involves converting the percentage to a decimal. To do this, simply divide the percentage by 100. 20% becomes 0.20 or 0.2. Then, multiply this decimal by the number:
0.2 * 14 = 2.8
This method is often quicker and easier, especially when dealing with larger numbers or more complex percentage calculations.
Method 3: Fraction Conversion
As mentioned earlier, 20% is equivalent to the fraction 1/5. Using this fraction, we can calculate 20% of 14 as follows:
(1/5) * 14 = 14/5 = 2.8
This method is particularly useful when dealing with percentages that have simple fractional equivalents, like 25% (1/4), 50% (1/2), or 75% (3/4).
Practical Applications of Percentages
Percentages are ubiquitous in daily life. Understanding how to calculate and interpret them is crucial for making informed decisions in various contexts:
- Shopping and Sales: Discount percentages are commonly used in retail. For example, a "20% off" sale means you'll pay 80% of the original price.
- Finance: Interest rates on loans and savings accounts are expressed as percentages. Understanding these percentages is vital for managing personal finances effectively.
- Taxes: Taxes are often calculated as a percentage of income or the value of goods and services.
- Statistics and Data Analysis: Percentages are extensively used to represent proportions and trends in data. For instance, opinion polls and survey results are frequently presented as percentages.
- Science and Engineering: Percentages are employed in various scientific and engineering applications, such as calculating efficiency, error margins, and concentration levels.
Expanding the Understanding: Beyond the Basics
While calculating 20% of 14 is straightforward, the underlying principles can be extended to more complex scenarios. Let's explore some of these:
- Calculating the Original Number: If you know a percentage of a number and the percentage itself, you can work backward to find the original number. For example, if 20% of a number is 2.8, then the original number is 2.8 / (20/100) = 14.
- Calculating Percentage Increase or Decrease: This is crucial for understanding changes over time. For example, if a quantity increases from 10 to 14, the percentage increase is calculated as: [(14-10)/10] * 100% = 40%.
- Compound Interest: This involves applying interest to both the principal amount and accumulated interest. Understanding compound interest is crucial for long-term financial planning.
- Proportions and Ratios: Percentages are closely related to proportions and ratios. They represent a comparative relationship between two quantities.
Advanced Concepts: Relationship to Other Mathematical Ideas
The concept of percentages is intrinsically linked to other mathematical areas:
- Algebra: Percentage problems can be represented and solved using algebraic equations.
- Calculus: Derivatives and integrals are used in advanced applications involving percentage changes and rates.
- Probability and Statistics: Percentages play a fundamental role in describing probabilities and statistical distributions.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when working with percentages?
A: Common mistakes include confusing percentages with decimals, incorrectly applying the formula, and misinterpreting percentage increases and decreases. Always double-check your calculations and ensure you understand the context of the problem.
Q: How can I improve my skills in calculating percentages?
A: Practice regularly! Start with simple problems and gradually work your way up to more complex scenarios. Utilize online calculators and resources to check your work and build your understanding.
Q: Are there any online tools or calculators that can help me with percentage calculations?
A: Many online calculators are available to assist with percentage calculations. These tools can be particularly helpful for more intricate problems. However, it's essential to understand the underlying principles to avoid dependency on these tools.
Q: What if the number isn't a whole number?
A: The methods described above work equally well with decimal numbers. You simply apply the same formula or conversion methods. For example, 20% of 14.5 would be 0.2 * 14.5 = 2.9.
Q: How can I apply percentages to real-world problems?
A: Consider tracking your monthly expenses and calculating what percentage is spent on each category (housing, food, transportation, etc.). This helps you visualize your spending habits and potentially identify areas for improvement. Similarly, you can apply this to budgeting, investment returns, and sales analysis.
Conclusion
Calculating 20 percent of 14, while seemingly simple, provides a gateway to understanding a fundamental mathematical concept with far-reaching applications. By mastering percentage calculations and grasping their relevance in various fields, you equip yourself with a valuable skill for navigating the complexities of everyday life and various professional fields. Remember to practice regularly, understand the underlying principles, and don't hesitate to use various methods to reinforce your learning. The journey of mastering percentages is not just about numbers; it's about developing a deeper understanding of the quantitative world around us.
Latest Posts
Latest Posts
-
Local Time Houston Texas Usa
Sep 20, 2025
-
160 Meters How Many Feet
Sep 20, 2025
-
60 Mg How Many Grams
Sep 20, 2025
-
Tan Inverse Of 3 4
Sep 20, 2025
-
80 000 Pounds To Kg
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.