9 2 As A Decimal
defexpoindia
Sep 22, 2025 · 5 min read
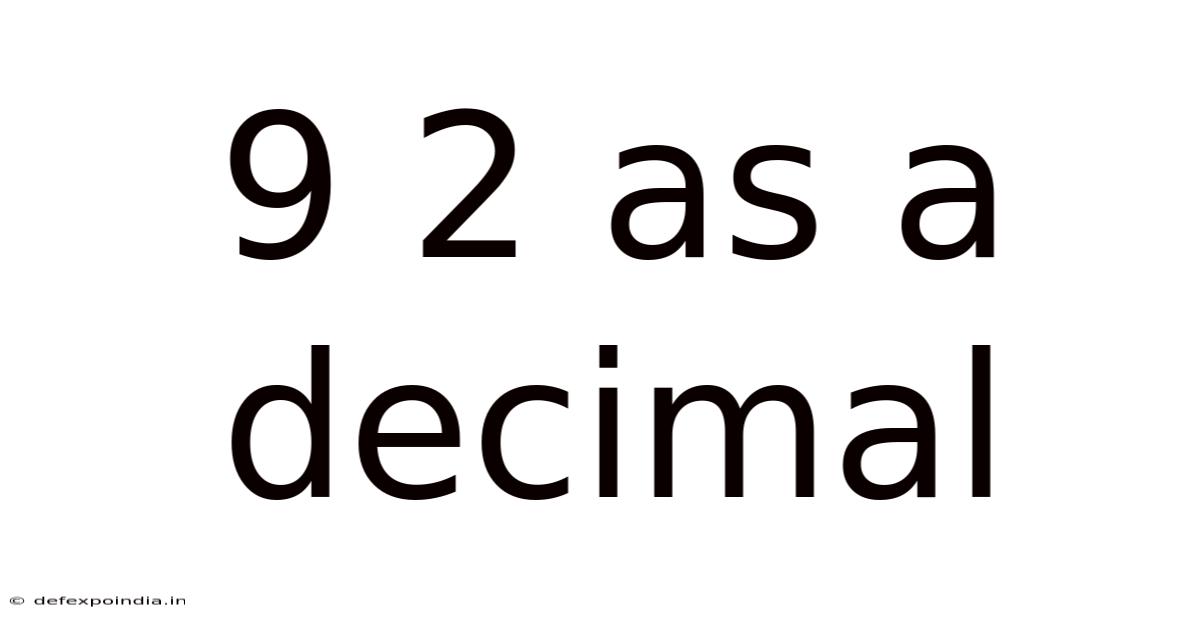
Table of Contents
9/2 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics. This article will delve deep into converting the fraction 9/2 into its decimal form, exploring various methods, underlying principles, and addressing common misconceptions. We'll also examine the broader implications of this conversion and its relevance in various mathematical contexts. By the end, you'll not only know the answer but also possess a deeper understanding of the relationship between fractions and decimals.
Understanding Fractions and Decimals
Before diving into the conversion of 9/2, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a number based on powers of 10, using a decimal point to separate the whole number part from the fractional part.
The fundamental relationship between fractions and decimals lies in their ability to represent the same value. Any fraction can be converted into a decimal, and vice versa, although some decimal representations may be non-terminating (i.e., they go on forever).
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. In this method, we divide the numerator by the denominator.
For 9/2, we perform the division:
9 ÷ 2 = 4 with a remainder of 1.
This means that 2 goes into 9 four times, with 1 remaining. To represent the remainder, we add a decimal point to the quotient (4) and continue the division by adding a zero to the remainder:
10 ÷ 2 = 5
Therefore, 9/2 = 4.5
Method 2: Equivalent Fractions
Another approach involves converting the fraction into an equivalent fraction with a denominator that is a power of 10. While not always feasible, this method can be particularly useful for certain fractions.
In this case, we can't easily find a whole number to multiply 2 by to get a power of 10 (10, 100, 1000, etc.). Therefore, this method isn't as efficient for 9/2 as long division.
Method 3: Using a Calculator
The simplest method, particularly for larger or more complex fractions, is to use a calculator. Simply enter 9 ÷ 2 and the calculator will directly provide the decimal equivalent: 4.5
Understanding the Result: 4.5
The result of converting 9/2 to a decimal is 4.5. This means that the fraction 9/2 represents the same quantity as the decimal 4.5. This decimal can be understood as 4 whole units and 5 tenths of a unit. Visually, imagine 4 whole objects and half (0.5) of another object.
9/2 in Different Contexts
The conversion of 9/2 to 4.5 has implications across various mathematical fields:
-
Geometry: If you're calculating the area of a rectangle with a length of 9 units and a width of 0.5 units, the area would be 4.5 square units.
-
Algebra: In solving equations, you might encounter fractions that need to be converted to decimals for easier manipulation. For example, an equation like x + 9/2 = 10 can be rewritten as x + 4.5 = 10, simplifying the solution process.
-
Data Analysis: When dealing with datasets, fractional data may be converted to decimal for easier analysis and representation in graphs and charts.
Decimal Representation and Terminating/Non-Terminating Decimals
It's important to note the difference between terminating and non-terminating decimals. A terminating decimal is a decimal that has a finite number of digits after the decimal point (e.g., 4.5, 2.75, 0.125). A non-terminating decimal, also known as a recurring decimal, has an infinite number of digits after the decimal point, with a repeating pattern (e.g., 1/3 = 0.333..., 1/7 = 0.142857142857...).
9/2 is an example of a terminating decimal because its decimal representation (4.5) has only one digit after the decimal point. This occurs because the denominator (2) is a factor of a power of 10 (10 = 2 x 5).
Common Misconceptions
A common misconception is that all fractions result in non-terminating decimals. This is incorrect. Fractions whose denominators only contain factors of 2 and 5 (or are powers of 2 and 5) will always result in terminating decimals. Fractions with other prime factors in their denominators (such as 3, 7, 11, etc.) often result in non-terminating decimals.
Further Exploration: Converting Decimals to Fractions
The process can also be reversed. To convert a decimal (like 4.5) back into a fraction:
- Write the decimal as a fraction with a denominator of 1: 4.5/1
- Multiply the numerator and denominator by a power of 10 to remove the decimal point: (4.5 x 10) / (1 x 10) = 45/10
- Simplify the fraction: 45/10 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 5. This gives us 9/2.
Frequently Asked Questions (FAQ)
-
Q: Can I convert 9/2 to a percentage?
- A: Yes, to convert a decimal to a percentage, multiply by 100. 4.5 x 100 = 450%.
-
Q: What if the fraction had a larger numerator or denominator?
- A: The long division method remains the same, although it might require more steps. Calculators are highly recommended for larger fractions.
-
Q: Are there other methods to convert fractions to decimals?
- A: While long division and using a calculator are the most common and practical methods, some advanced techniques exist, such as using continued fractions, which are beyond the scope of this introductory guide.
-
Q: Why is understanding fraction to decimal conversion important?
- A: This conversion is fundamental in various mathematical applications, including algebra, geometry, data analysis, and everyday calculations. It allows for greater flexibility and easier manipulation of numerical values.
Conclusion
Converting 9/2 to its decimal equivalent, 4.5, is a straightforward process achievable through long division, the use of a calculator, or, less efficiently in this case, by finding an equivalent fraction with a denominator that's a power of 10. Understanding this conversion is critical for a solid foundation in mathematics and its practical applications. Remember the key difference between terminating and non-terminating decimals, and the significance of the denominator's prime factorization in determining the type of decimal representation. This knowledge empowers you to confidently tackle various mathematical challenges and provides a deeper understanding of the interconnectedness of fractions and decimals.
Latest Posts
Latest Posts
-
How Many Grams Is 2000mg
Sep 22, 2025
-
Convert 38 Inches To Centimeters
Sep 22, 2025
-
1 1 8 To Metric
Sep 22, 2025
-
What Is 140lb In Kg
Sep 22, 2025
-
1 8 Mile To Feet
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 9 2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.