7 8 As A Percentage

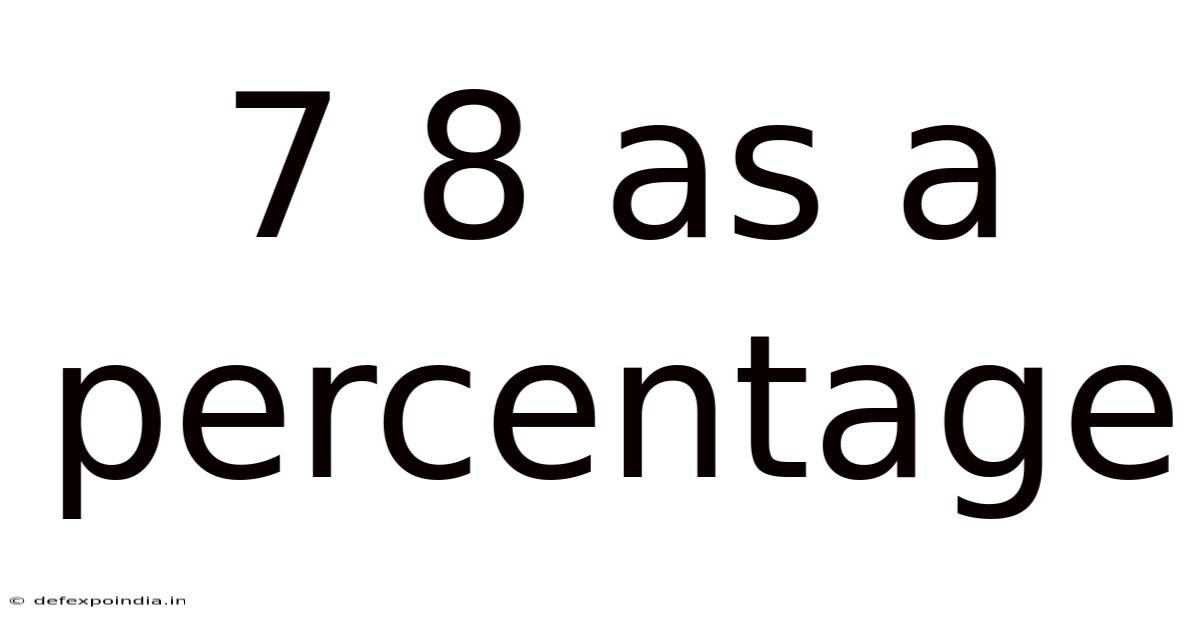
Decoding 7/8 as a Percentage: A full breakdown

Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in a store to understanding financial reports. This thorough look will delve deep into the conversion of the fraction 7/8 into a percentage, explaining the process step-by-step and providing valuable context for further understanding of percentage calculations. We'll explore different methods, address common misconceptions, and offer practical examples to solidify your knowledge. This article will equip you with the tools to confidently tackle similar fraction-to-percentage conversions And it works..

Understanding Fractions and Percentages

Before we dive into converting 7/8 into a percentage, let's briefly review the concepts of fractions and percentages. Worth adding: it's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). Here's a good example: in the fraction 7/8, 7 is the numerator and 8 is the denominator. A fraction represents a part of a whole. This means we have 7 parts out of a total of 8 equal parts Surprisingly effective..

A percentage, on the other hand, represents a fraction out of 100. Also, the symbol "%" signifies "per hundred. " That's why, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are a convenient way to express proportions and comparisons Turns out it matters..

Method 1: Direct Conversion using Division

The most straightforward way to convert a fraction to a percentage is through division. Follow these steps:

Divide the numerator by the denominator: Divide 7 by 8. This calculation yields 0.875.
Multiply the result by 100: Multiply 0.875 by 100. This gives you 87.5.
Add the percentage symbol: The final answer is 87.5% Not complicated — just consistent..

That's why, 7/8 is equal to 87.5%.

Method 2: Finding an Equivalent Fraction with a Denominator of 100

This method involves finding an equivalent fraction where the denominator is 100. While less efficient than direct division for simple fractions, this approach provides a valuable understanding of the underlying principles:

Determine the multiplication factor: To convert the denominator of 7/8 (which is 8) to 100, we need to find a number that, when multiplied by 8, results in 100. There isn't a whole number that achieves this perfectly, but we can still use this principle for illustrative purposes And that's really what it comes down to. Still holds up..
Find an approximation: To obtain a denominator close to 100, we can multiply 8 by 12.5. Doing this will not give us exactly 100, but 100 is a desirable denominator when converting to percentages.
Apply the multiplication factor to the numerator: We multiply the numerator (7) by the same factor (12.5). This yields 87.5.
Express as a percentage: The resulting fraction is 87.5/100, which is equivalent to 87.5%. Note: This method demonstrates the core concept of equivalent fractions in the context of percentage calculation, but the slight imprecision in not reaching a perfect denominator of 100 highlights the advantages of the direct division method.

Method 3: Using a Calculator

Modern calculators greatly simplify the conversion process. Because of that, simply enter 7 ÷ 8 and then multiply the result by 100. That said, most calculators will display the answer as 87. 5%. This method is quick and efficient, especially for more complex fractions No workaround needed..

Practical Applications of 7/8 as a Percentage (87.5%)

The knowledge that 7/8 equals 87.5% has numerous real-world applications:

Discounts: If a store offers an 87.5% discount on an item, you know it's equivalent to a 7/8 reduction Worth keeping that in mind..
Surveys and polls: If 7 out of 8 people surveyed preferred a certain product, the result can be expressed as an 87.5% preference rate Not complicated — just consistent..
Progress tracking: If you've completed 7 out of 8 tasks, you've made 87.5% progress.
Financial analysis: Understanding percentages is crucial for interpreting financial statements and calculating returns on investment.

Addressing Common Misconceptions

A frequent misunderstanding is confusing fractions with percentages. On the flip side, while intrinsically linked, they are distinct representations. A fraction expresses a part-to-whole relationship directly, while a percentage expresses the same relationship relative to 100 Simple, but easy to overlook..

Another common mistake is incorrectly performing the division or multiplication steps during the conversion. Double-checking your calculations is always recommended to avoid errors Small thing, real impact..

Expanding Understanding: Working with Other Fractions

The methods described above can be applied to any fraction. The key is to understand the fundamental principle: divide the numerator by the denominator and then multiply by 100 to obtain the percentage equivalent. For example:

1/4 = 0.25 * 100 = 25%
3/5 = 0.6 * 100 = 60%
5/6 = 0.8333... * 100 ≈ 83.33%

Frequently Asked Questions (FAQ)

Q: Why do we multiply by 100 when converting a fraction to a percentage?

A: Because a percentage is a fraction expressed out of 100. Multiplying by 100 scales the decimal representation of the fraction to a value out of 100.
Q: Can I convert any fraction into a percentage?

A: Yes, any fraction can be converted into a percentage using the methods explained above.
Q: What if the resulting percentage has a long decimal?

A: You can round the decimal to a suitable number of decimal places depending on the context. Take this: 83.Worth adding: 333... % can be rounded to 83.33% That alone is useful..

Conclusion

Converting 7/8 into a percentage is a straightforward process that involves dividing the numerator by the denominator and multiplying the result by 100. In practice, this yields 87. On top of that, 5%. In real terms, understanding this conversion is essential for various mathematical and real-world applications. By mastering this fundamental skill, you'll develop a stronger foundation in mathematical concepts and improve your ability to analyze and interpret data expressed in both fractional and percentage forms. Remember to practice regularly to solidify your understanding and enhance your problem-solving abilities. The more you practice, the more comfortable and confident you will become in tackling similar conversions and further exploring the fascinating world of mathematics The details matter here..