4 5 As A Percentage
defexpoindia
Sep 23, 2025 · 5 min read
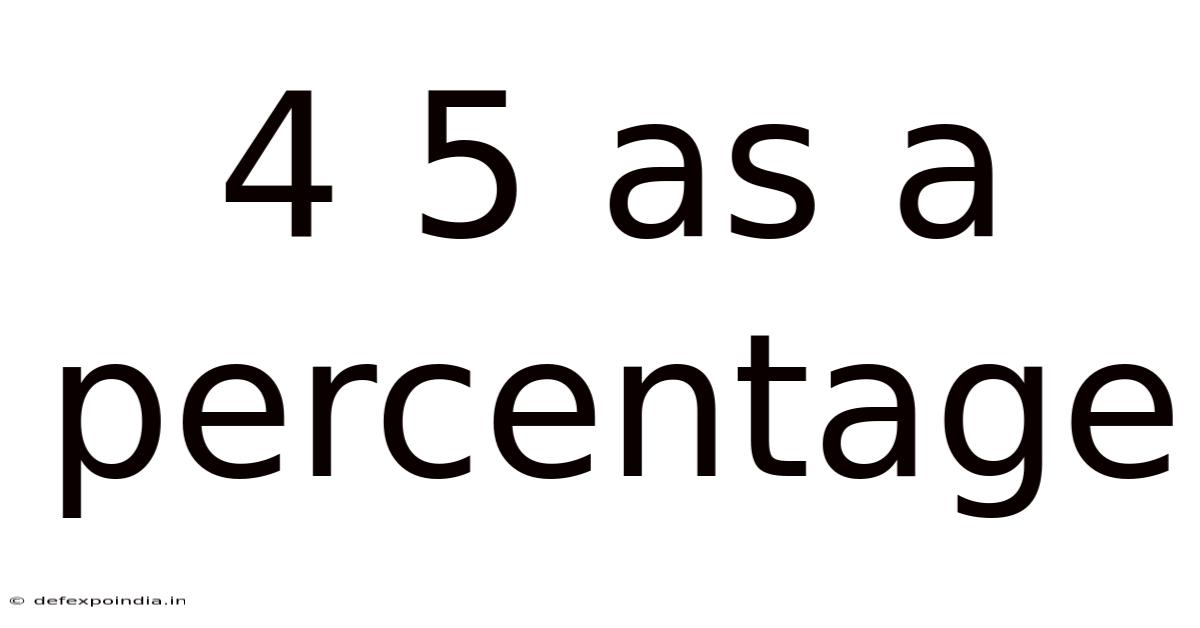
Table of Contents
Understanding 4/5 as a Percentage: A Comprehensive Guide
Many everyday situations require converting fractions to percentages. Understanding how to do this is crucial for various applications, from calculating grades to understanding financial data. This comprehensive guide will walk you through the process of converting the fraction 4/5 into a percentage, explaining the underlying mathematical principles and providing various methods to achieve the same result. We'll also explore practical applications and address common questions. This will equip you with the knowledge to confidently tackle similar fraction-to-percentage conversions in the future.
Understanding Fractions and Percentages
Before diving into the conversion, let's review the basics. A fraction represents a part of a whole. In the fraction 4/5, the top number (4) is the numerator, representing the number of parts we have, and the bottom number (5) is the denominator, representing the total number of parts in the whole.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
The key to converting fractions to percentages is to express the fraction as an equivalent fraction with a denominator of 100.
Method 1: Converting the Fraction Directly to a Percentage
This is the most straightforward method. To convert 4/5 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by finding a number that, when multiplied by the denominator (5), equals 100.
That number is 20 (because 5 x 20 = 100). To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by 20:
(4 x 20) / (5 x 20) = 80/100
Since 80/100 represents 80 out of 100, the percentage equivalent of 4/5 is 80%.
Method 2: Converting the Fraction to a Decimal, then to a Percentage
This method involves two steps. First, we convert the fraction 4/5 to a decimal by dividing the numerator (4) by the denominator (5):
4 ÷ 5 = 0.8
Next, we convert the decimal 0.8 to a percentage by multiplying it by 100:
0.8 x 100 = 80
Therefore, 4/5 is equal to 80%. This method is particularly useful when dealing with fractions that don't easily convert to an equivalent fraction with a denominator of 100.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. We can set up a proportion where x represents the percentage we want to find:
4/5 = x/100
To solve for x, we can cross-multiply:
5x = 400
Then, divide both sides by 5:
x = 80
Therefore, 4/5 is equal to 80%. This method is helpful for understanding the underlying relationship between fractions and percentages.
Practical Applications of Converting 4/5 to a Percentage
Understanding how to convert fractions like 4/5 to percentages has numerous real-world applications:
- Calculating Grades: If you answered 4 out of 5 questions correctly on a test, your score is 80%.
- Financial Calculations: Understanding percentages is crucial for calculating interest rates, discounts, taxes, and profit margins. For instance, if a store offers a 20% discount, the remaining price is 80% of the original price (equivalent to 4/5).
- Data Analysis: Percentages are widely used in representing data in charts and graphs, making it easier to compare proportions.
- Everyday Life: Percentages are used in cooking recipes (e.g., 80% lean ground beef), expressing probabilities, and understanding statistics.
Further Exploration: Working with Other Fractions
The methods described above can be applied to convert any fraction to a percentage. For instance, let's consider converting 3/4 to a percentage:
- Method 1 (Direct Conversion): Multiply both numerator and denominator by 25 (since 4 x 25 = 100): (3 x 25) / (4 x 25) = 75/100 = 75%
- Method 2 (Decimal Conversion): 3 ÷ 4 = 0.75; 0.75 x 100 = 75%
- Method 3 (Proportions): 3/4 = x/100; 4x = 300; x = 75%
Similarly, converting fractions like 1/3 or 2/7 requires slightly more complex calculations as they don't directly convert to fractions with a denominator of 100. In these cases, the decimal conversion method is often more efficient. For instance, 1/3 ≈ 0.333... which is approximately 33.33%. The recurring decimal emphasizes that the conversion to a percentage is an approximation in such instances.
Frequently Asked Questions (FAQ)
Q: Why is it important to understand fraction-to-percentage conversions?
A: Understanding these conversions is essential for various aspects of daily life, academic studies, and professional work. It allows for a clearer understanding of proportions, facilitating better decision-making and data interpretation.
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have the functionality to perform this conversion. Simply divide the numerator by the denominator and then multiply the result by 100.
Q: What if the fraction has a large denominator?
A: For fractions with large denominators that don't easily convert to a denominator of 100, the decimal conversion method is usually the most efficient.
Q: Are there any online tools that can perform this conversion?
A: Yes, numerous online calculators and converters are available to assist with fraction-to-percentage conversions. However, understanding the underlying mathematical principles is crucial for better comprehension and problem-solving.
Q: What if the fraction is an improper fraction (numerator > denominator)?
A: The same methods apply. Convert the improper fraction to a mixed number or decimal before applying the conversion techniques to obtain a percentage greater than 100%. For instance, 5/4 = 1.25, and 1.25 * 100% = 125%.
Conclusion
Converting 4/5 to a percentage is a fundamental skill with wide-ranging applications. This guide presented three different methods to achieve this conversion, emphasizing the importance of understanding the underlying mathematical principles. By mastering these methods, you can confidently tackle similar conversions and apply this knowledge in various real-world scenarios. Remember, practice makes perfect, so continue practicing with different fractions to solidify your understanding. The ability to convert fractions to percentages is a valuable tool that enhances your mathematical proficiency and problem-solving capabilities.
Latest Posts
Latest Posts
-
20 Feet How Many Meters
Sep 23, 2025
-
Cuantas Pulgadas Son 23 Cm
Sep 23, 2025
-
Convert 70 Fahrenheit To Celsius
Sep 23, 2025
-
Whats 40 C In Fahrenheit
Sep 23, 2025
-
How Far Is 130 Yards
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 4 5 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.