5 16 As A Decimal
defexpoindia
Sep 21, 2025 · 5 min read
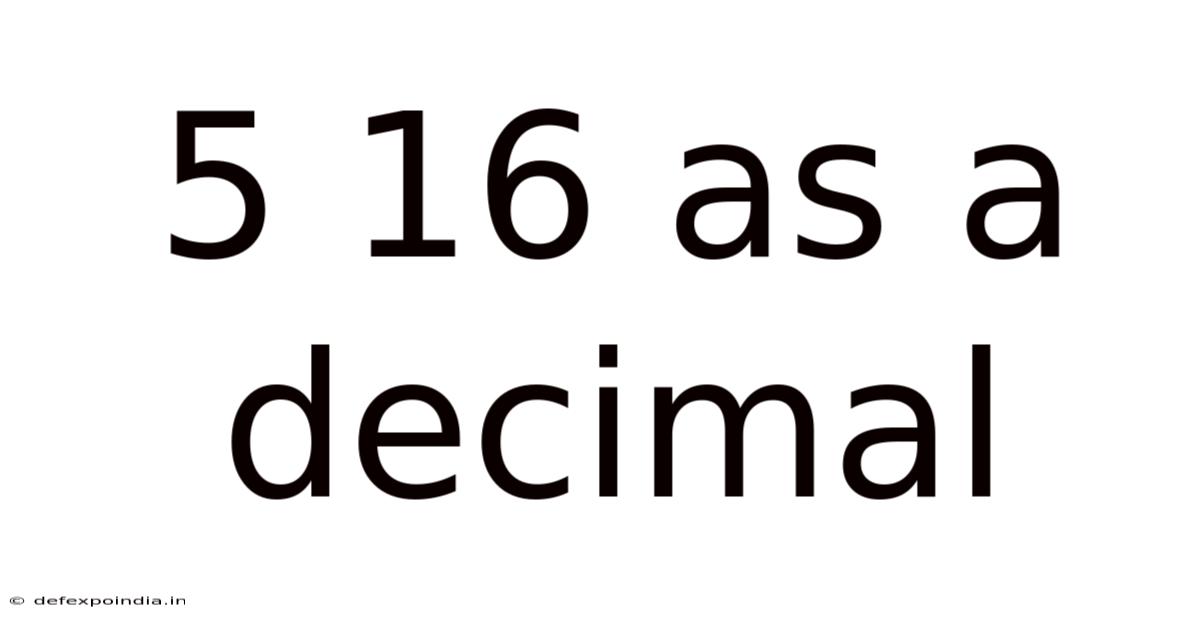
Table of Contents
Understanding 5/16 as a Decimal: A Comprehensive Guide
Many everyday situations require converting fractions to decimals. Whether you're working on a DIY project, calculating a percentage, or simply solving a math problem, understanding how to convert fractions like 5/16 to decimals is a crucial skill. This comprehensive guide will not only show you how to convert 5/16 to a decimal but also delve into the underlying principles, provide multiple methods for solving similar problems, and answer frequently asked questions.
Introduction: Decimals and Fractions
Before we dive into the specifics of converting 5/16, let's briefly recap the relationship between decimals and fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal is another way to represent a part of a whole, using a base-ten system. The decimal point separates the whole number part from the fractional part. Converting between fractions and decimals is essentially translating between these two representation systems.
Method 1: Long Division
The most fundamental method for converting a fraction to a decimal is through long division. We divide the numerator (5) by the denominator (16).
-
Set up the long division: Write 5 (the numerator) inside the long division symbol and 16 (the denominator) outside. Add a decimal point followed by zeros after the 5 to allow for continued division.
16 | 5.0000 -
Divide: 16 goes into 5 zero times. Write a 0 above the 5.
0 16 | 5.0000 -
Bring down the next digit: Bring down the 0 next to the 5, making it 50.
0 16 | 5.0000 -
Continue the division: 16 goes into 50 three times (16 x 3 = 48). Write the 3 above the 0. Subtract 48 from 50, leaving a remainder of 2.
0.3 16 | 5.0000 -48 2 -
Bring down the next digit and repeat: Bring down another 0 to make it 20. 16 goes into 20 once (16 x 1 = 16). Write the 1 above the next 0. Subtract 16 from 20, leaving a remainder of 4.
0.31 16 | 5.0000 -48 20 -16 4 -
Continue the process: Continue this process, bringing down zeros and dividing until you reach the desired level of accuracy or the remainder becomes zero. In this case, we'll continue for a few more steps:
0.3125 16 | 5.0000 -48 20 -16 40 -32 80 -80 0
Therefore, 5/16 as a decimal is 0.3125.
Method 2: Using a Calculator
The easiest way to convert a fraction to a decimal is by using a calculator. Simply divide the numerator (5) by the denominator (16). Most calculators will directly provide the decimal equivalent: 0.3125.
Method 3: Understanding Decimal Place Value
While long division and calculators are efficient, understanding the underlying decimal place value system helps solidify comprehension. Consider the fraction 5/16. We can think of this as 5 parts out of 16 equal parts. To convert this to a decimal, we need to express it as a sum of tenths, hundredths, thousandths, and so on. Although this method is less practical for complex fractions, it builds a strong understanding of the relationship between fractions and decimals. This method is less efficient for this particular problem but illustrates the concept.
Explanation: Why 0.3125?
The decimal 0.3125 represents:
- 0: No whole numbers.
- 3: Three tenths (3/10)
- 1: One hundredth (1/100)
- 2: Two thousandths (2/1000)
- 5: Five ten-thousandths (5/10000)
Adding these together, we get 3/10 + 1/100 + 2/1000 + 5/10000 = 0.3125
Working with Different Fractions
The methods described above – long division, calculator use, and understanding place value – can be applied to convert any fraction to a decimal. For example, let's consider some other fractions:
- 1/4: Using long division or a calculator gives us 0.25.
- 3/8: Long division yields 0.375.
- 7/10: This is already a decimal, 0.7, as the denominator is a power of 10.
- 1/3: This results in a recurring decimal, 0.3333... This is because the division doesn't terminate.
Recurring Decimals
It's important to note that some fractions result in recurring decimals. These are decimals that repeat a sequence of digits infinitely. For example, 1/3 is 0.3333..., and 1/7 is 0.142857142857... When dealing with recurring decimals, we often round them to a specific number of decimal places based on the context.
Frequently Asked Questions (FAQ)
Q1: Why is it important to understand fraction to decimal conversion?
A1: Converting fractions to decimals is essential in numerous fields, including:
- Mathematics: Solving equations, comparing fractions, and understanding percentages.
- Science: Many scientific measurements involve decimals.
- Engineering: Precision calculations and design often require decimal values.
- Finance: Calculating interest rates, discounts, and other financial calculations.
- Everyday life: Measuring ingredients in cooking, calculating distances, and understanding proportions.
Q2: What if the fraction has a larger numerator than denominator?
A2: If the numerator is larger than the denominator, the resulting decimal will be a number greater than 1. For example, 7/4 = 1.75. The whole number part represents the quotient of the division, and the decimal part represents the remainder.
Q3: How can I improve my skills in converting fractions to decimals?
A3: Practice is key! Work through numerous examples using different fractions, both simple and complex. Start with easy fractions and gradually progress to more challenging ones. Use both long division and a calculator to reinforce your understanding. Focus on understanding the underlying principles rather than just memorizing the results.
Q4: Are there any online tools or resources for converting fractions to decimals?
A4: Many online calculators and converters are available. These tools can be beneficial for verifying your calculations and practicing different conversions. However, understanding the underlying methods is crucial for building a strong foundation in mathematics.
Conclusion:
Converting fractions to decimals is a fundamental skill in mathematics with broad applications. While calculators provide a quick solution, understanding the process of long division and the concept of decimal place value is crucial for a deeper understanding of the mathematical relationships involved. Mastering this skill opens doors to more complex mathematical concepts and applications in various fields. Remember to practice regularly to build proficiency and confidence. Through consistent effort and a solid understanding of the principles, converting fractions like 5/16 to their decimal equivalent (0.3125) becomes straightforward and even enjoyable.
Latest Posts
Latest Posts
-
500 Percent As A Decimal
Sep 22, 2025
-
How Big Is 32 Centimeters
Sep 22, 2025
-
Xncxx Mm To Inches Calculator
Sep 22, 2025
-
Convert 45 Centimeters To Meters
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.