500 Percent As A Decimal
defexpoindia
Sep 22, 2025 · 5 min read
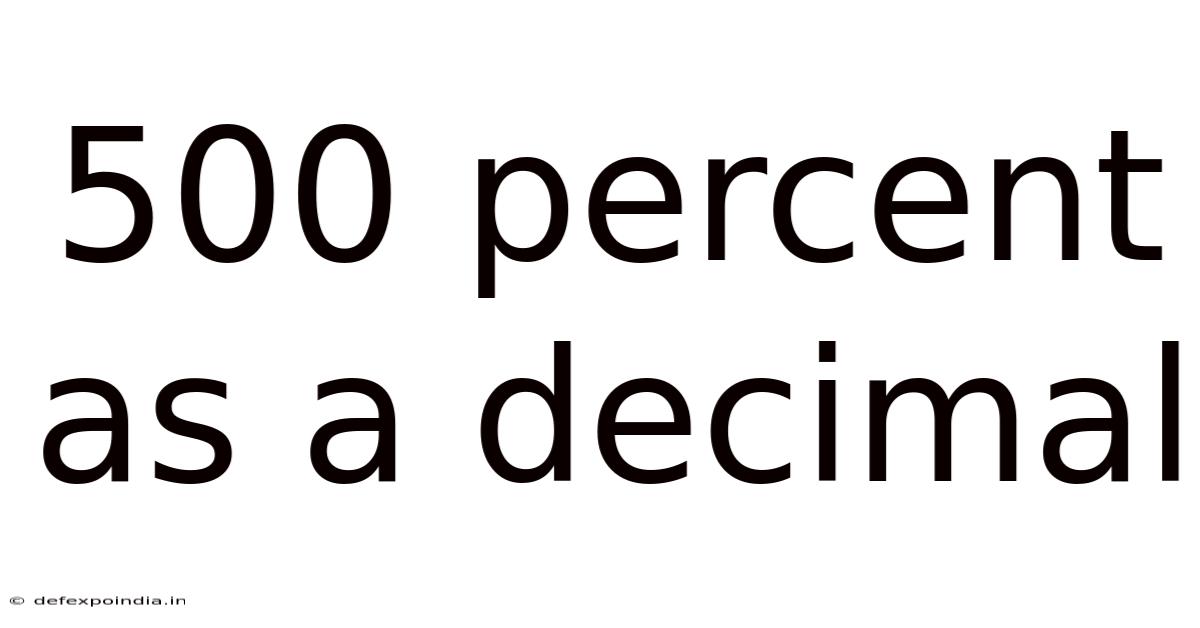
Table of Contents
500 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is fundamental to many areas, from everyday finances to advanced scientific calculations. This article will delve deep into the conversion of 500 percent to its decimal form, exploring the underlying principles, providing practical examples, and addressing common questions. We'll unpack the concept thoroughly, ensuring you gain a solid understanding not just of this specific conversion but of percentage-to-decimal conversions in general. By the end, you’ll be confident in handling similar conversions and applying this knowledge across various disciplines.
Understanding Percentages
Before we dive into converting 500 percent to a decimal, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." So, 50 percent (50%) means 50 out of 100, or 50/100. This fraction can be simplified to 1/2, or expressed as a decimal, 0.5.
This fundamental concept underpins all percentage calculations. Understanding this relationship between fractions, percentages, and decimals is key to mastering these conversions.
Converting Percentages to Decimals: The Basic Method
The conversion of a percentage to a decimal is a straightforward process. The key is to remember that the percentage represents a fraction with a denominator of 100. To convert a percentage to a decimal, you simply divide the percentage by 100.
The Formula:
Percentage / 100 = Decimal
Example: Let's convert 25% to a decimal.
25% / 100 = 0.25
This works because dividing by 100 is equivalent to moving the decimal point two places to the left. If you're dealing with a whole number percentage like 25%, the decimal point is implicitly at the end (25.0). Moving it two places to the left gives you 0.25.
500 Percent as a Decimal: The Conversion
Now, let's apply this knowledge to our specific question: What is 500 percent as a decimal?
Using the formula:
500% / 100 = 5.0
Therefore, 500% as a decimal is 5.0 or simply 5. This might seem counterintuitive at first; a percentage above 100% might seem unusual. However, percentages above 100% simply represent values greater than the whole.
Understanding Percentages Greater Than 100%
Percentages greater than 100% represent values exceeding the original whole. This frequently arises in contexts like:
- Growth and Increase: If a company's profits increase by 150%, it means its profits are now 250% of their original value.
- Financial Investments: If an investment yields a return of 300%, it means the investment's value has tripled.
- Statistical Comparisons: In comparing data sets, one set might be 120% the size of another.
- Scaling and Ratios: In various scientific and engineering applications, values can exceed 100% of a reference value.
Practical Examples of Percentages Greater than 100%
Let's illustrate with some real-world examples:
- Investment Growth: You invest $1000, and your investment grows by 200%. This means your investment increased by $2000 (200% of $1000), resulting in a total of $3000.
- Population Increase: A town's population increased by 110%. If the original population was 5000, the increase is 5500 (110% of 5000), resulting in a new population of 10500.
- Production Output: A factory increased its production by 350%. If the initial output was 100 units, the increase is 350 units (350% of 100 units), resulting in a total output of 450 units.
Beyond the Basics: Fractions and Percentages
While the decimal conversion is straightforward, it's helpful to understand the relationship between percentages, decimals, and fractions. We've already established that a percentage is a fraction out of 100. To reinforce this, let's revisit the 500% example:
500% = 500/100 = 5/1 = 5
This clearly shows that 500% represents five times the original value.
Working with Percentages in Calculations
Percentages are frequently used in calculations. Here are some common applications:
- Calculating Percentages of Amounts: To find a percentage of a number, convert the percentage to a decimal and multiply it by the number. For example, 20% of 50 is 0.20 * 50 = 10.
- Calculating Percentage Increase/Decrease: This involves finding the difference between two values, dividing the difference by the original value, and multiplying by 100 to express it as a percentage.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
Frequently Asked Questions (FAQ)
Q1: Can a percentage be greater than 100%?
A1: Yes, absolutely. Percentages greater than 100% represent values exceeding the original whole.
Q2: What is the easiest way to convert a percentage to a decimal?
A2: The easiest method is to divide the percentage by 100, or simply move the decimal point two places to the left.
Q3: How do I convert a decimal back to a percentage?
A3: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
Q4: What are some real-world applications of percentages above 100%?
A4: Real-world applications include calculating growth rates, investment returns, population changes, and scaling factors in various fields.
Q5: Is there a limit to how high a percentage can be?
A5: Theoretically, there's no upper limit to a percentage. It can be any positive number, representing any multiple of the original value.
Conclusion
Converting 500 percent to a decimal, resulting in 5.0, is a straightforward application of a fundamental mathematical concept. This conversion, and the understanding of percentages in general, is crucial for navigating various aspects of life, from personal finance to professional applications. By grasping the principles outlined in this guide, you'll be equipped to confidently handle percentages, regardless of their magnitude. Remember the simple formula: Percentage / 100 = Decimal, and you'll be well on your way to mastering this important skill. The ability to fluently convert between percentages and decimals is a valuable asset in numerous contexts, solidifying your understanding of numerical representation and enhancing your problem-solving abilities across diverse fields. Remember to practice regularly to build your confidence and proficiency!
Latest Posts
Latest Posts
-
How Many Pounds In 120kg
Sep 22, 2025
-
160 Kg To Lbs Weight
Sep 22, 2025
-
How Many Feet Is 7m
Sep 22, 2025
-
Whats 40 Inches In Feet
Sep 22, 2025
-
How Long Is 48 Cm
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 500 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.