5 1/2 As A Decimal
defexpoindia
Sep 23, 2025 · 5 min read
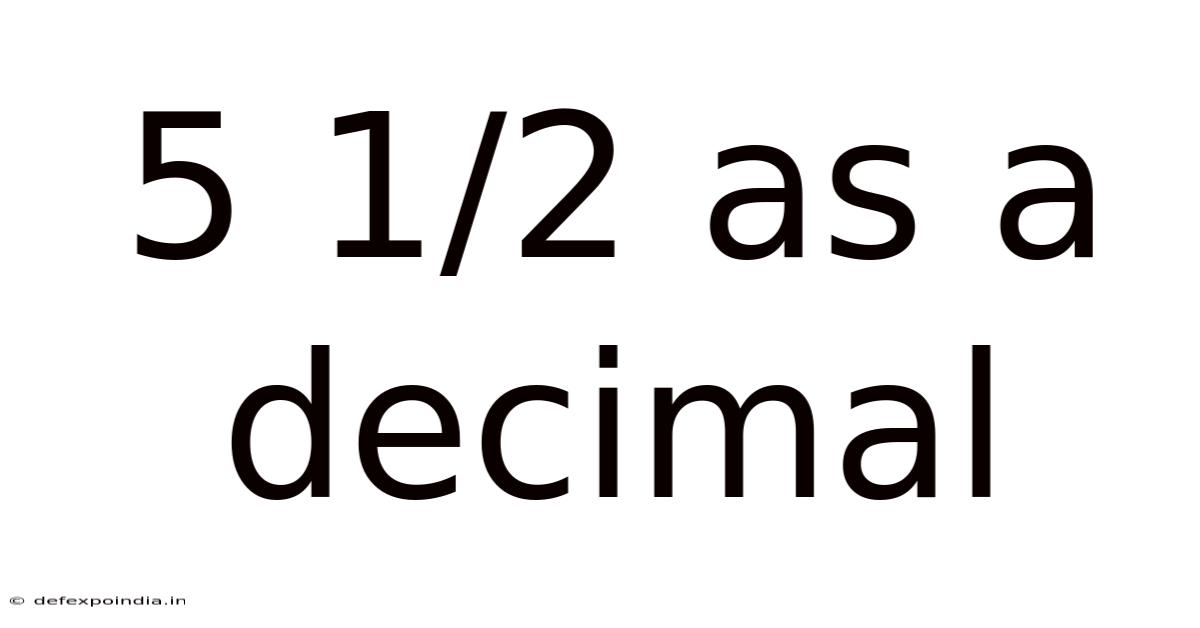
Table of Contents
Decoding 5 1/2: A Comprehensive Guide to Understanding Mixed Numbers as Decimals
Understanding how to convert mixed numbers, like 5 1/2, into decimals is a fundamental skill in mathematics. This seemingly simple conversion is crucial for various applications, from everyday calculations to advanced scientific computations. This comprehensive guide will explore the process of converting 5 1/2 to its decimal equivalent, delve into the underlying mathematical principles, and offer practical examples to solidify your understanding. We'll also address common questions and misconceptions surrounding this conversion.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion, let's define our terms. A mixed number combines a whole number and a fraction, like 5 1/2. A decimal represents a number in base-10, using a decimal point to separate the whole number part from the fractional part. For example, 5.5 is a decimal. The core of converting a mixed number to a decimal is transforming the fractional part into its decimal representation.
Converting 5 1/2 to a Decimal: The Step-by-Step Approach
There are several ways to convert 5 1/2 to a decimal. Let's explore two common methods:
Method 1: Converting the Fraction to a Decimal
This method focuses on converting the fractional part (1/2) into a decimal first and then adding it to the whole number part (5).
-
Understand the Fraction: The fraction 1/2 represents one part out of two equal parts.
-
Divide the Numerator by the Denominator: To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). In this case, we divide 1 by 2: 1 ÷ 2 = 0.5
-
Add the Whole Number: Now, add the decimal equivalent of the fraction to the whole number: 5 + 0.5 = 5.5
Therefore, 5 1/2 as a decimal is 5.5.
Method 2: Converting the Mixed Number to an Improper Fraction
This method involves first transforming the mixed number into an improper fraction and then converting that improper fraction into a decimal.
-
Convert to an Improper Fraction: An improper fraction has a numerator larger than or equal to its denominator. To convert 5 1/2 to an improper fraction:
- Multiply the whole number (5) by the denominator of the fraction (2): 5 x 2 = 10
- Add the numerator of the fraction (1) to the result: 10 + 1 = 11
- Keep the same denominator (2): The improper fraction is 11/2
-
Divide the Numerator by the Denominator: Divide the numerator (11) by the denominator (2): 11 ÷ 2 = 5.5
Again, we arrive at the decimal equivalent: 5.5
Understanding the Underlying Mathematical Principles
The process of converting fractions to decimals relies on the fundamental concept of division. A fraction, at its core, represents a division problem. The numerator is the dividend (the number being divided), and the denominator is the divisor (the number dividing the dividend). When we perform this division, the result is the decimal equivalent of the fraction.
In the case of 5 1/2, we are essentially dividing one part into two equal parts. This division inherently implies the concept of proportions and ratios. The fraction 1/2 represents a ratio of 1 to 2, meaning one part for every two total parts. This ratio is equivalent to 0.5 in decimal form.
Practical Applications of Decimal Conversion
Converting mixed numbers to decimals is essential in many real-world scenarios:
-
Financial Calculations: Calculating amounts of money often involves dealing with fractional parts of currency units. For instance, understanding 5 1/2 dollars as $5.50 is crucial for accurate financial transactions.
-
Measurement: Measurements often include fractional parts. Converting these fractions to decimals simplifies calculations and comparisons. For example, 5 1/2 inches converted to 5.5 inches makes calculations involving multiple measurements much easier.
-
Scientific Computations: Many scientific formulas and calculations use decimals. Converting measurements or data points expressed as mixed numbers into decimal form is often a necessary step in these calculations.
-
Data Analysis: In data analysis, having consistent numerical formats is important. Converting mixed numbers to decimals helps ensure uniformity and facilitates the use of statistical software.
-
Everyday Calculations: Even simple tasks like calculating cooking ingredients (e.g., 5 1/2 cups of flour) or dividing items equally among people benefit from the ease of decimal arithmetic.
Beyond 5 1/2: Converting Other Mixed Numbers
The methods described above can be applied to convert any mixed number into its decimal equivalent. Here are a few examples:
- 3 1/4: 1/4 = 0.25; 3 + 0.25 = 3.25
- 2 3/5: 3/5 = 0.6; 2 + 0.6 = 2.6
- 1 7/8: 7/8 = 0.875; 1 + 0.875 = 1.875
Remember, the key steps are to:
- Convert the fraction to a decimal by dividing the numerator by the denominator.
- Add the resulting decimal to the whole number part of the mixed number.
Frequently Asked Questions (FAQs)
Q1: What if the fraction results in a repeating decimal?
A1: Some fractions, like 1/3 (which equals 0.333...), result in repeating decimals. In these cases, you can either use the repeating decimal representation (e.g., 0.3̅) or round to a specific number of decimal places based on the context of your problem.
Q2: Can I use a calculator to convert mixed numbers to decimals?
A2: Yes, most calculators have the functionality to perform this conversion directly. You can either input the mixed number using the fraction button or convert the mixed number to an improper fraction before dividing.
Q3: Is there any difference between 5.5 and 5 1/2?
A3: Mathematically, there is no difference. They represent the same quantity; 5.5 is simply the decimal representation of the mixed number 5 1/2. The choice of representation often depends on the context and the preference of the user.
Conclusion: Mastering Decimal Conversions
Converting mixed numbers like 5 1/2 to decimals is a fundamental skill that streamlines calculations and enhances our understanding of numbers. By mastering this process, you are not only equipping yourself with a practical mathematical tool but also strengthening your foundation in numerical operations. Remember that the key to success lies in understanding the underlying principles of fractions, decimals, and the relationship between them. With practice and consistent application, converting mixed numbers to decimals will become second nature. Whether you're tackling financial calculations, scientific problems, or everyday tasks, this skill will prove invaluable in your mathematical journey.
Latest Posts
Latest Posts
-
12 Millimeters On A Ruler
Sep 23, 2025
-
400 Degree F To C
Sep 23, 2025
-
How Tall Is 64 Inches
Sep 23, 2025
-
8 Inches Converted To Mm
Sep 23, 2025
-
152 Cm Convert To Inches
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.