4 1/8 As A Decimal
defexpoindia
Sep 23, 2025 · 5 min read
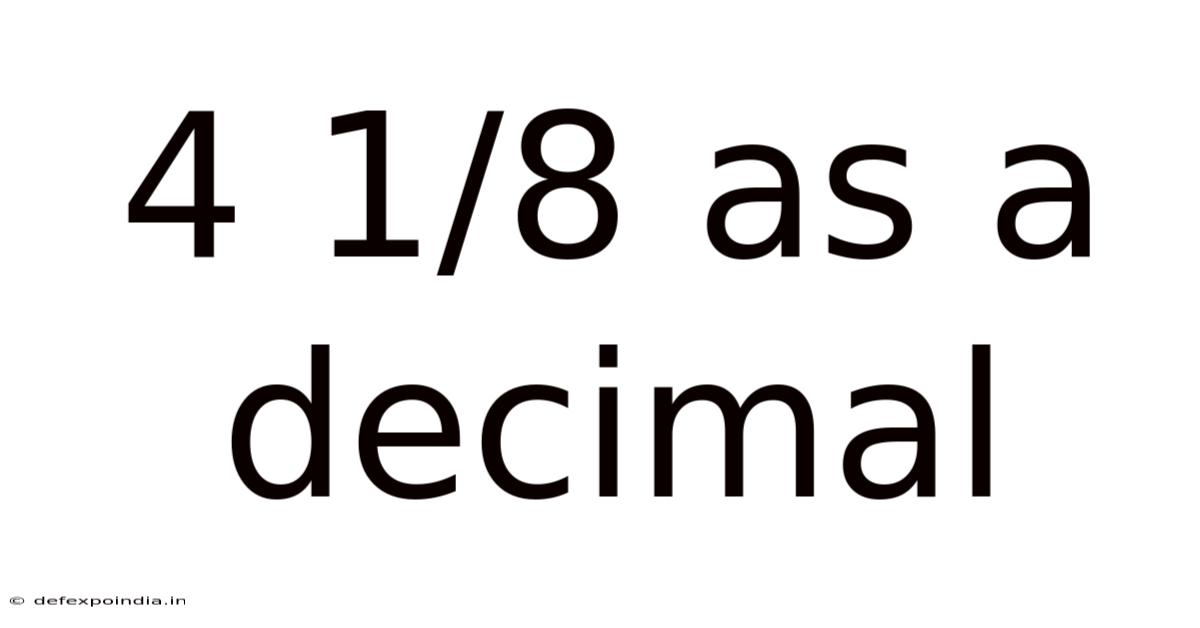
Table of Contents
Understanding 4 1/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will explore the conversion of the mixed number 4 1/8 into its decimal equivalent, providing a step-by-step process, explaining the underlying principles, and addressing frequently asked questions. This will equip you with a solid understanding not only of this specific conversion but also of the broader concept of fraction-to-decimal conversion.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's review some basic concepts. A mixed number combines a whole number and a fraction, like 4 1/8. The whole number represents a complete unit, while the fraction represents a part of a unit. In this case, we have four whole units and one-eighth of another unit. A fraction, on the other hand, expresses a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
Method 1: Converting the Fraction to a Decimal then Adding the Whole Number
This is the most straightforward approach. We'll first convert the fractional part (1/8) to a decimal and then add the whole number (4).
-
Divide the numerator by the denominator: To convert 1/8 to a decimal, we perform the division 1 ÷ 8. This gives us 0.125.
-
Add the whole number: Now, add the whole number 4 to the decimal value we just obtained: 4 + 0.125 = 4.125
Therefore, 4 1/8 as a decimal is 4.125.
Method 2: Converting the Mixed Number to an Improper Fraction, then to a Decimal
This method involves converting the mixed number into an improper fraction first – a fraction where the numerator is larger than the denominator. This approach is particularly useful when dealing with more complex mixed numbers.
-
Convert to an improper fraction: To convert 4 1/8 to an improper fraction, we multiply the whole number (4) by the denominator (8), add the numerator (1), and then place the result over the original denominator: (4 * 8) + 1 = 33. The improper fraction is 33/8.
-
Divide the numerator by the denominator: Now, divide the numerator (33) by the denominator (8): 33 ÷ 8 = 4.125
Again, we arrive at the decimal equivalent of 4.125.
Method 3: Using Decimal Equivalents of Common Fractions
For common fractions, it's often helpful to memorize their decimal equivalents. Knowing that 1/8 = 0.125 significantly speeds up the process. This approach is best for frequently encountered fractions. If you know that 1/8 is 0.125, you can immediately add the whole number 4 to get 4.125.
The Significance of Decimal Representation
Converting fractions to decimals offers several advantages:
-
Ease of comparison: Decimals allow for easier comparison of values than fractions, particularly when fractions have different denominators. For instance, comparing 4 1/8 with other numbers in decimal form simplifies the process.
-
Computational efficiency: Decimals simplify calculations, especially with the aid of calculators and computers. Many mathematical operations, like addition, subtraction, multiplication, and division, are more readily performed with decimals.
-
Real-world applications: Decimals are widely used in various real-world applications, including measurements, finance, and scientific data representation. Understanding decimal equivalents of fractions is therefore crucial for practical applications.
Explanation of the Process: A Deeper Dive
The process of converting a fraction to a decimal fundamentally involves division. The fraction represents a division problem: the numerator is divided by the denominator. This division results in a decimal value, representing the fractional part as a portion of one whole. The decimal system uses powers of 10 (tenths, hundredths, thousandths, etc.) to represent fractional parts, making it a convenient and universally understood system for representing numbers.
Frequently Asked Questions (FAQs)
-
Q: Can all fractions be converted to exact decimal equivalents?
- A: No. Fractions with denominators that are not factors of powers of 10 (e.g., 2, 5, 10, 20, 50, etc.) may result in repeating or non-terminating decimals. For example, 1/3 converts to 0.3333... (a repeating decimal). However, 1/8, as demonstrated, converts to a terminating decimal.
-
Q: What if the fraction is negative?
- A: If the fraction is negative (e.g., -4 1/8), the resulting decimal will also be negative (-4.125). The conversion process remains the same; simply apply the negative sign to the final result.
-
Q: Are there any other methods to convert fractions to decimals?
- A: While the methods described above are the most common and practical, more advanced techniques exist, particularly for complex fractions and those involving algebraic expressions. These often utilize concepts from advanced mathematics.
-
Q: How can I improve my fraction-to-decimal conversion skills?
- A: Practice is key! Regularly work through different examples, starting with simple fractions and gradually progressing to more complex ones. Memorizing decimal equivalents of common fractions will also significantly speed up the process. Utilize online resources and practice exercises to reinforce your understanding.
Conclusion
Converting 4 1/8 to its decimal equivalent, 4.125, is a simple yet illustrative example of a fundamental mathematical skill. Understanding the different methods, the underlying principles, and addressing common questions provides a complete picture of this essential conversion. Mastering this skill is not just about getting the right answer; it's about understanding the relationship between fractions and decimals, which is crucial for various applications in mathematics and beyond. The ability to confidently convert fractions to decimals enhances your problem-solving abilities and opens the door to tackling more complex mathematical challenges. Through practice and a clear understanding of the principles involved, you can confidently navigate the world of fractions and decimals with ease and precision. Remember, consistent practice is the key to mastering this important mathematical concept.
Latest Posts
Latest Posts
-
Cuanto Es 1 5 Kg
Sep 23, 2025
-
What Is 40g In Ounces
Sep 23, 2025
-
9 Pulgadas Cuantos Cm Son
Sep 23, 2025
-
29 Degree Celsius To Fahrenheit
Sep 23, 2025
-
What Is 19 In Inches
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 4 1/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.