3 4 As A Percent
defexpoindia
Sep 23, 2025 · 6 min read
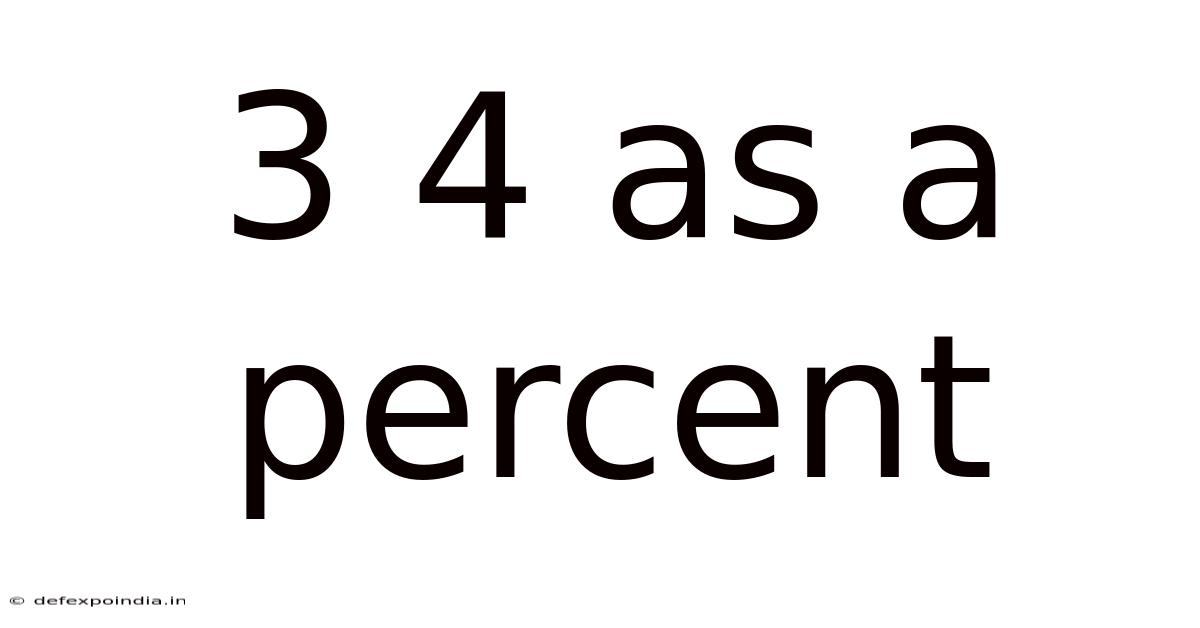
Table of Contents
Understanding 3/4 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, crucial for various applications in daily life, from calculating discounts to understanding financial reports. This article provides a comprehensive guide to understanding 3/4 as a percent, exploring various methods for conversion, and delving into the practical applications of this knowledge. We'll explore the core concepts, step-by-step calculations, and even touch upon more advanced related topics. By the end, you'll not only know that 3/4 is 75%, but also why it is and how you can apply this knowledge effectively.
What is a Percentage?
Before diving into the conversion of 3/4, let's clarify the concept of a percentage. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Percentages are used to express proportions or ratios in a standardized and easily comparable format.
Method 1: Converting a Fraction to a Decimal, then to a Percentage
This is a common and straightforward method to convert a fraction like 3/4 into a percentage. It involves two simple steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, you divide the numerator (the top number) by the denominator (the bottom number). In the case of 3/4, we perform the division:
3 ÷ 4 = 0.75
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, you multiply the decimal by 100 and add the "%" symbol. So, for 0.75:
0.75 x 100 = 75%
Therefore, 3/4 is equal to 75%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method utilizes the concept of equivalent fractions. Equivalent fractions represent the same proportion but have different numerators and denominators. The goal here is to find an equivalent fraction of 3/4 that has a denominator of 100.
To do this, we ask ourselves: "What number, when multiplied by 4, equals 100?" The answer is 25 (4 x 25 = 100). Since we multiply the denominator by 25, we must also multiply the numerator by 25 to maintain the same proportion:
(3 x 25) / (4 x 25) = 75/100
Since 75/100 means 75 out of 100, this is equivalent to 75%.
Method 3: Using Proportions
Proportions offer a more formal approach to solving this problem. A proportion is a statement that two ratios are equal. We can set up a proportion to find the percentage equivalent of 3/4:
3/4 = x/100
To solve for x (the percentage), we cross-multiply:
4x = 300
x = 300 ÷ 4
x = 75
Therefore, 3/4 is equal to 75%.
Understanding the Relationship Between Fractions, Decimals, and Percentages
It's essential to understand the interconnectedness of fractions, decimals, and percentages. They are different ways of representing the same value. The ability to convert between these forms is crucial for various mathematical operations and problem-solving.
- Fractions: Represent a part of a whole using a numerator and a denominator.
- Decimals: Represent a part of a whole using a base-ten system.
- Percentages: Represent a part of a whole as a number out of 100.
Practical Applications of Understanding 3/4 as 75%
The knowledge that 3/4 is equal to 75% has numerous practical applications:
- Sales and Discounts: A 75% discount means you pay only 25% of the original price. Understanding this equivalence is crucial for making informed purchasing decisions.
- Financial Calculations: Interest rates, investment returns, and loan payments are often expressed as percentages. Converting fractions to percentages helps in making accurate financial calculations.
- Data Analysis: In statistics and data analysis, understanding percentage representation is essential for interpreting data and drawing meaningful conclusions. Representing data as percentages allows for easy comparison and interpretation.
- Everyday Life: Many everyday situations involve percentages, such as calculating tips, measuring ingredients in cooking, or understanding survey results.
Advanced Concepts and Related Topics
Moving beyond the basic conversion, let's explore some related concepts that build upon this foundational understanding:
- Working with Percentages Greater Than 100%: Percentages can also be greater than 100%, representing values exceeding the whole. For example, if a company's sales increased by 150% it means they increased by 1.5 times the original value.
- Calculating Percentage Increases and Decreases: Understanding percentage changes involves calculating the difference between two values and expressing this difference as a percentage of the original value. For instance, if a price increases from $100 to $125, the percentage increase is 25% (($25/$100)*100).
- Percentage Points vs. Percentage Change: These are frequently confused terms. A percentage point refers to an arithmetic difference between two percentages, while a percentage change refers to the relative change expressed as a percentage of the original value. For instance, an increase from 10% to 15% is a 5 percentage point increase but a 50% percentage change ((5%/10%)*100).
- Compound Interest: This involves calculating interest on the principal amount plus accumulated interest from previous periods. Understanding percentages is crucial for calculating compound interest accurately. This concept is fundamental to long-term investments and loans.
- Statistical Significance: In statistical analysis, percentages help determine the significance of results. For instance, in A/B testing, the percentage difference in conversion rates between two groups can indicate if one approach is significantly better than the other.
Frequently Asked Questions (FAQs)
Q: Can I convert any fraction to a percentage?
A: Yes, you can convert any fraction to a percentage using the methods described above. The process involves dividing the numerator by the denominator to get a decimal and then multiplying the decimal by 100 to get the percentage.
Q: What if I have a mixed number (e.g., 1 3/4)?
A: First convert the mixed number into an improper fraction. For 1 3/4, this would be 7/4 (1 x 4 + 3 = 7). Then, follow the steps for converting a fraction to a percentage. 7/4 = 1.75 = 175%.
Q: Are there any online calculators that can help with this?
A: While this article focuses on manual calculations to promote understanding, many online calculators can perform fraction-to-percentage conversions. However, mastering the process manually is beneficial for comprehension and problem-solving skills.
Q: Why is understanding percentages important in real-world applications?
A: Percentages provide a standardized and easily comparable way to represent proportions and ratios. They are used extensively in various fields, including finance, business, statistics, and everyday life. Understanding percentages empowers informed decision-making.
Conclusion
Understanding 3/4 as 75% is not just about memorizing a conversion; it's about grasping the fundamental principles of fractions, decimals, and percentages. The ability to convert between these forms is a valuable mathematical skill applicable in numerous contexts. By mastering these conversions and exploring the related concepts discussed, you'll be well-equipped to handle various mathematical challenges and confidently apply percentage calculations in your daily life and professional endeavors. Remember, the key lies not just in knowing the answer but in understanding the underlying why and how.
Latest Posts
Latest Posts
-
How High Is 80 Meters
Sep 23, 2025
-
Cuanto Es 1 5 Kg
Sep 23, 2025
-
What Is 40g In Ounces
Sep 23, 2025
-
9 Pulgadas Cuantos Cm Son
Sep 23, 2025
-
29 Degree Celsius To Fahrenheit
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 4 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.