What Percent Is 2 6
defexpoindia
Sep 19, 2025 · 5 min read
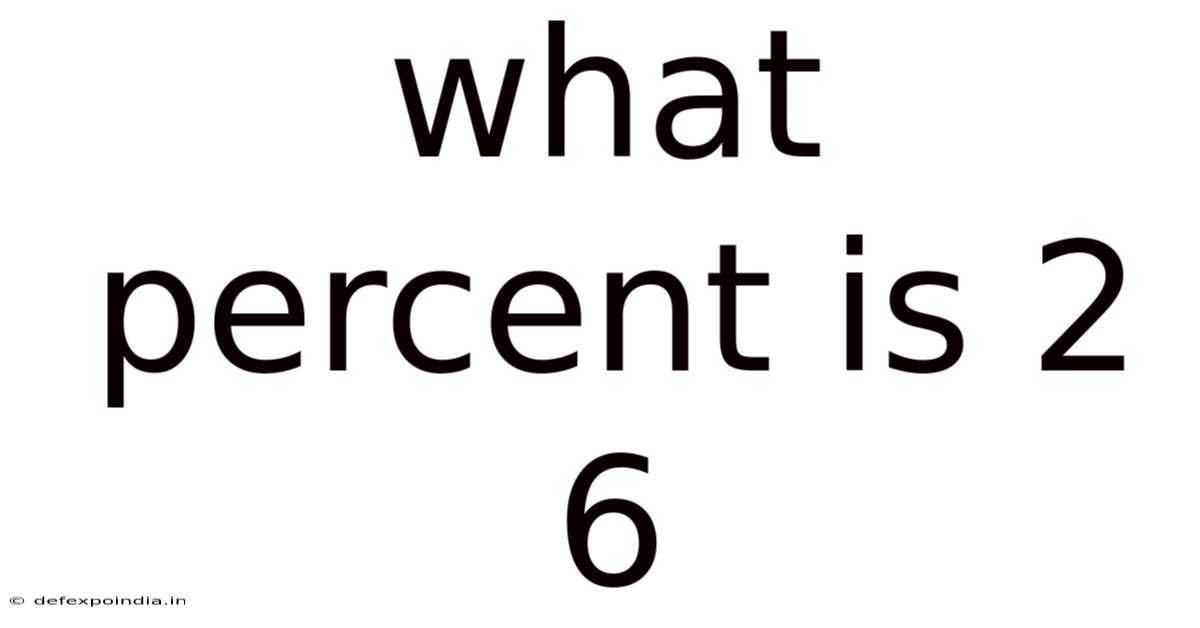
Table of Contents
What Percent is 2 of 6? Understanding Ratios, Fractions, and Percentages
This article will delve into the seemingly simple question: "What percent is 2 of 6?" While the answer might seem immediately obvious to some, understanding the underlying concepts of ratios, fractions, and percentages is crucial for a firm grasp of mathematics and its applications in everyday life. We'll explore the calculation, provide different approaches to solving the problem, and discuss the broader implications of percentage calculations. This comprehensive guide is designed for learners of all levels, from those just beginning to explore percentages to those seeking a deeper understanding of the mathematical principles involved.
Understanding the Fundamentals: Ratios, Fractions, and Percentages
Before diving into the calculation, let's establish a solid foundation. These three concepts—ratios, fractions, and percentages—are closely intertwined and represent different ways of expressing the same relationship between two numbers.
-
Ratio: A ratio is a comparison of two quantities. It shows the relative size of one quantity compared to another. We can express a ratio using a colon (:) or the word "to." For instance, the ratio of 2 to 6 can be written as 2:6 or 2 to 6.
-
Fraction: A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The fraction representing 2 out of 6 is 2/6.
-
Percentage: A percentage is a fraction expressed as a part of 100. It indicates how many parts out of 100 represent a certain proportion. The symbol "%" represents "per cent," meaning "out of 100."
These three concepts are interchangeable. A ratio can be converted into a fraction, and a fraction can be converted into a percentage, and vice versa. This flexibility allows us to solve problems using the method most comfortable and efficient for a given situation.
Calculating the Percentage: What Percent is 2 of 6?
Now, let's tackle the core question: what percent is 2 of 6? There are several ways to approach this calculation:
Method 1: Using a Proportion
This method utilizes the concept of equivalent ratios. We can set up a proportion:
2/6 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x,' we cross-multiply:
6x = 200
Then, divide both sides by 6:
x = 200/6 = 33.333...
Therefore, 2 is approximately 33.33% of 6.
Method 2: Converting the Fraction to a Decimal, then to a Percentage
First, convert the fraction 2/6 to a decimal by dividing the numerator (2) by the denominator (6):
2 ÷ 6 = 0.333...
Next, multiply the decimal by 100 to convert it to a percentage:
0.333... × 100 = 33.333...%
This confirms our previous result.
Method 3: Simplifying the Fraction First
Before converting to a percentage, we can simplify the fraction 2/6. Both the numerator and the denominator are divisible by 2:
2/6 = 1/3
Now, converting 1/3 to a decimal:
1 ÷ 3 = 0.333...
Multiplying by 100 to get the percentage:
0.333... × 100 = 33.333...%
Simplifying the fraction beforehand can make the calculation easier, especially with larger numbers.
Understanding the Result: 33.33%
The result, approximately 33.33%, tells us that 2 represents one-third (1/3) of 6. This percentage signifies the proportional relationship between the two numbers. In practical terms, if you have a group of 6 items, and you select 2 of them, you have selected approximately 33.33% of the total.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in many real-world situations:
- Finance: Calculating interest rates, discounts, taxes, and profit margins.
- Retail: Determining sale prices, markups, and profit percentages.
- Science: Expressing experimental results, statistical data, and concentrations.
- Everyday Life: Calculating tips, understanding nutritional information, and interpreting survey results.
Frequently Asked Questions (FAQ)
Q: Why is the percentage a repeating decimal (33.333...%)?
A: The percentage is a repeating decimal because the fraction 1/3 is a rational number with a denominator that cannot be expressed as a power of 10. This means its decimal representation is non-terminating (it goes on forever) and repeating.
Q: Can I round the percentage to 33%?
A: While rounding to 33% is acceptable in some contexts, it introduces a slight inaccuracy. The more precise representation is 33.33%, or even better, 33.333...% to indicate the repeating decimal nature. The level of precision required depends on the specific application.
Q: What if I had a different ratio, like 3 out of 8? How would I calculate the percentage?
A: You would follow the same steps as outlined above. Convert the ratio 3/8 into a decimal by dividing 3 by 8 (0.375), then multiply the result by 100 to obtain the percentage (37.5%).
Q: Are there any online calculators or tools that can help me calculate percentages?
A: Many online calculators are available that can quickly calculate percentages. These tools can be helpful for checking your work or for solving more complex percentage problems. However, understanding the underlying principles is crucial for applying percentage calculations effectively.
Conclusion: Mastering Percentages
This article has demonstrated various methods for calculating the percentage represented by 2 out of 6, highlighting the importance of understanding ratios, fractions, and their interconversion. Mastering percentage calculations is a valuable skill applicable across diverse fields. While simple calculators can provide quick answers, a deep understanding of the underlying mathematical principles allows for greater flexibility, accuracy, and problem-solving capabilities in various contexts. Remember to choose the method that best suits your comfort level and the complexity of the problem. Practice is key to building confidence and proficiency in working with percentages. By understanding these core concepts, you are well-equipped to tackle more complex percentage problems and apply this knowledge to real-world scenarios.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Is 2 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.