What Is 1/4 In Percentage
defexpoindia
Sep 19, 2025 · 6 min read
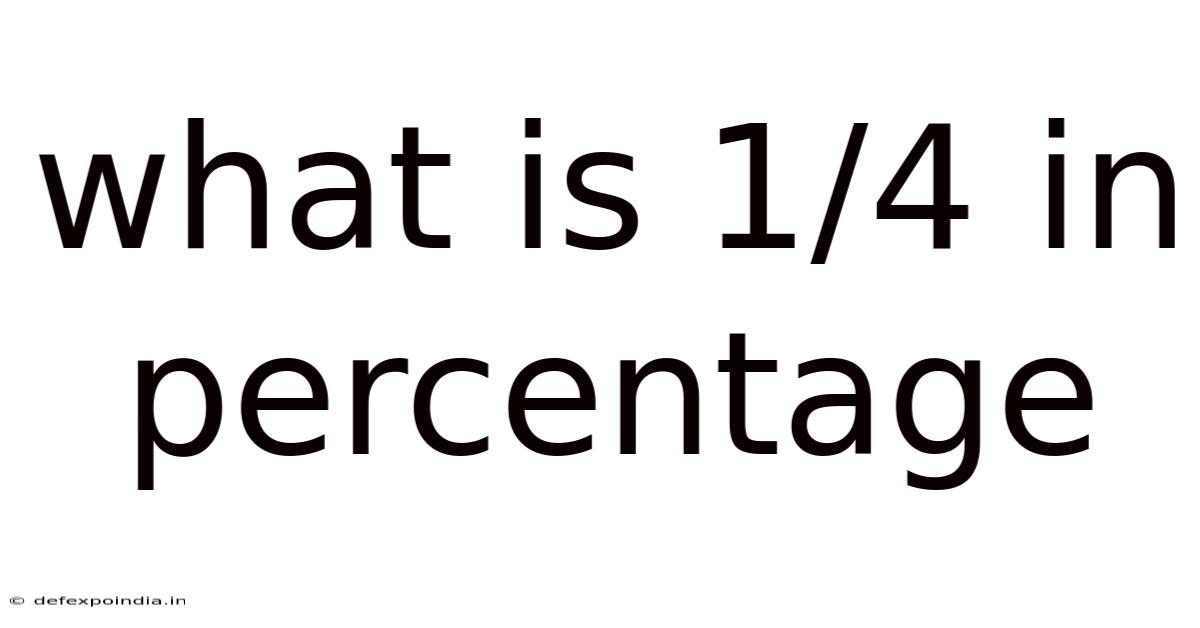
Table of Contents
What is 1/4 in Percentage? A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into the conversion of the fraction 1/4 into a percentage, exploring the underlying principles and providing practical examples to solidify your understanding. We'll cover not only the calculation itself but also explore related concepts and answer frequently asked questions. By the end, you'll confidently convert any fraction into a percentage.
Understanding Fractions and Percentages
Before diving into the conversion of 1/4, let's briefly review the core concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 1/4, 1 is the numerator and 4 is the denominator. This means we have 1 part out of a total of 4 equal parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It's a way to express a proportion or ratio as a number out of 100. For instance, 25% means 25 out of 100, which can also be written as the fraction 25/100.
Converting 1/4 to a Percentage: The Steps
The conversion of a fraction to a percentage involves two simple steps:
Step 1: Convert the fraction to a decimal. To do this, divide the numerator by the denominator.
In the case of 1/4:
1 ÷ 4 = 0.25
Step 2: Convert the decimal to a percentage. To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
0.25 x 100 = 25%
Therefore, 1/4 is equal to 25%.
Visualizing 1/4 as 25%
Imagine a pizza cut into four equal slices. If you take one slice, you have 1/4 of the pizza. Since there are four slices in total, and each slice represents 25% (100% / 4 slices = 25% per slice), one slice is equivalent to 25% of the whole pizza. This visual representation helps to solidify the connection between the fraction and the percentage.
Real-World Applications of 1/4 and 25%
The equivalence of 1/4 and 25% has numerous applications in daily life. Here are a few examples:
-
Sales and Discounts: A 25% discount on an item means you're paying only three-quarters (3/4 or 75%) of the original price. If an item costs $100, a 25% discount would reduce the price by $25 (100 x 0.25 = 25), leaving the final price at $75.
-
Baking and Cooking: Many recipes use fractions to represent ingredient quantities. Understanding the percentage equivalent can help in adjusting recipes for different needs. For example, if a recipe calls for 1/4 cup of sugar, you know it's equivalent to 25% of a cup.
-
Financial Calculations: Percentages are widely used in finance. Understanding fractions helps in interpreting financial data and making informed decisions. For example, understanding that interest rates are often expressed as percentages helps in comparing different investment options.
-
Data Analysis and Statistics: Percentages are crucial for expressing proportions and trends in data. Being able to convert fractions to percentages makes it easier to interpret data presented in different formats.
Understanding Other Fraction to Percentage Conversions
The process of converting fractions to percentages remains consistent regardless of the fraction's complexity. Let's explore a few more examples:
- 1/2: 1 ÷ 2 = 0.5; 0.5 x 100 = 50%
- 3/4: 3 ÷ 4 = 0.75; 0.75 x 100 = 75%
- 1/5: 1 ÷ 5 = 0.2; 0.2 x 100 = 20%
- 2/5: 2 ÷ 5 = 0.4; 0.4 x 100 = 40%
- 1/10: 1 ÷ 10 = 0.1; 0.1 x 100 = 10%
These examples demonstrate the consistent application of the two-step process: divide the numerator by the denominator to obtain the decimal, and then multiply the decimal by 100 to find the percentage.
Explaining the Mathematics Behind the Conversion
The conversion from fraction to percentage is fundamentally a change of representation; it doesn't alter the underlying value. We are simply expressing the same proportion in different formats. The key to this conversion lies in the fact that a percentage is a fraction with a denominator of 100.
When we divide the numerator by the denominator in a fraction, we are essentially finding the decimal equivalent that represents the proportion. Multiplying this decimal by 100 is equivalent to finding the equivalent fraction with a denominator of 100, thereby obtaining the percentage.
For example, consider the fraction 1/4. By dividing 1 by 4, we obtain 0.25. Multiplying 0.25 by 100 gives us 25, which represents 25/100 or 25%. This shows how the mathematical operations are directly linked to the concept of finding an equivalent fraction with a denominator of 100.
Frequently Asked Questions (FAQ)
Q1: What if the fraction results in a repeating decimal?
A1: Some fractions, such as 1/3 (which equals 0.333...), result in repeating decimals. In these cases, you can round the decimal to a certain number of decimal places before converting to a percentage. For example, 1/3 can be approximated as 0.33, which converts to 33%.
Q2: Can I convert percentages back into fractions?
A2: Absolutely! To convert a percentage back into a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 25% becomes 25/100, which simplifies to 1/4.
Q3: Are there any shortcuts for converting common fractions to percentages?
A3: Yes, with practice, you'll quickly memorize the percentage equivalents of common fractions like 1/2 (50%), 1/4 (25%), 3/4 (75%), and 1/10 (10%). This will significantly speed up your calculations.
Q4: Why is understanding this conversion important?
A4: This conversion is fundamental to many areas of life, from understanding financial statements to interpreting data and making informed decisions in various contexts. It's a crucial building block for further mathematical studies.
Conclusion
Converting 1/4 to a percentage (25%) is a simple yet essential mathematical skill. Understanding the process—dividing the numerator by the denominator and then multiplying by 100—allows you to confidently convert any fraction to its percentage equivalent. This skill is widely applicable in daily life and forms a foundation for more advanced mathematical concepts. By mastering this fundamental conversion, you'll enhance your mathematical proficiency and broaden your ability to interpret numerical information efficiently and effectively. Remember, practice is key, so try converting other fractions to percentages to further solidify your understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1/4 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.