8 7/8 As A Decimal
defexpoindia
Sep 23, 2025 · 5 min read
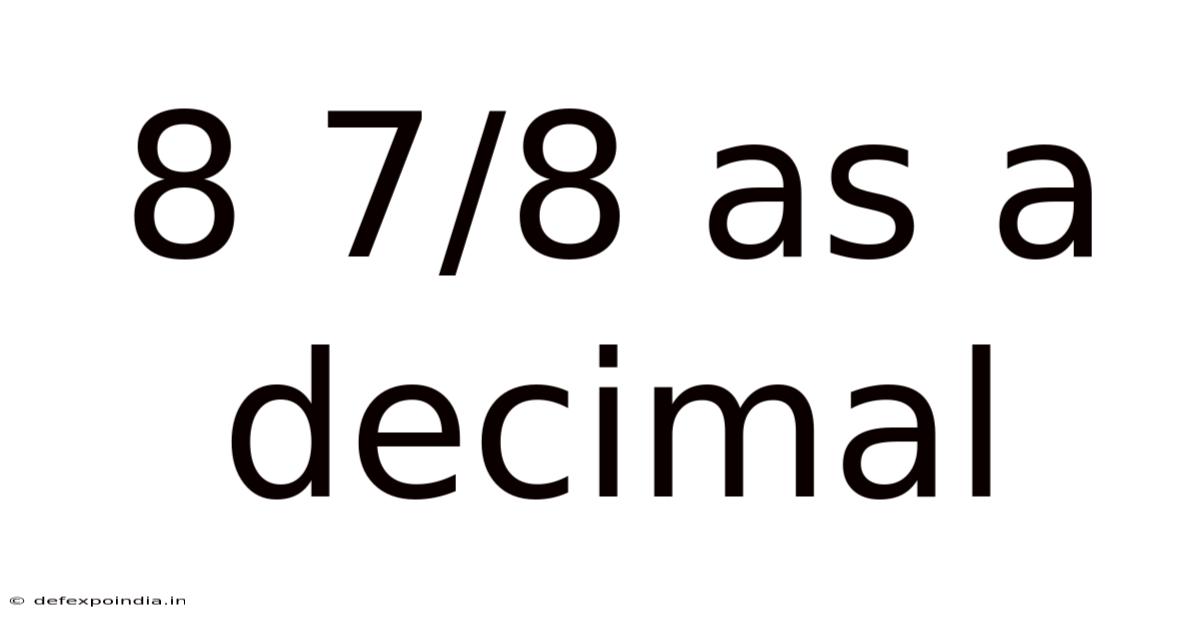
Table of Contents
8 7/8 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications in science, engineering, and everyday life. This article delves into the conversion of the mixed number 8 7/8 into its decimal equivalent, providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing common questions. We'll also explore different methods to achieve this conversion, ensuring a comprehensive understanding for learners of all levels. This guide aims to clarify this seemingly simple conversion, offering deeper insights into the process and its broader mathematical context.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's briefly recap the concepts of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 8 7/8. The whole number represents a complete unit, while the fraction represents a part of a unit. A decimal, on the other hand, represents a number using base-10, where each digit to the right of the decimal point represents a power of ten (tenths, hundredths, thousandths, etc.).
Method 1: Converting the Fraction to a Decimal First
This is perhaps the most straightforward method. We first convert the fraction 7/8 into a decimal and then add the whole number 8.
Step 1: Divide the Numerator by the Denominator
To convert 7/8 to a decimal, we perform the division: 7 ÷ 8.
This division results in 0.875.
Step 2: Add the Whole Number
Now, we add the whole number 8 to the decimal we just obtained:
8 + 0.875 = 8.875
Therefore, 8 7/8 as a decimal is 8.875.
Method 2: Converting the Entire Mixed Number Directly
This method involves converting the entire mixed number into an improper fraction before dividing.
Step 1: Convert to an Improper Fraction
To convert 8 7/8 into an improper fraction, we multiply the whole number (8) by the denominator (8) and then add the numerator (7). This result becomes the new numerator, while the denominator remains the same.
(8 * 8) + 7 = 64 + 7 = 71
So, 8 7/8 becomes 71/8.
Step 2: Divide the Numerator by the Denominator
Now, we divide the numerator (71) by the denominator (8):
71 ÷ 8 = 8.875
Again, we arrive at the decimal equivalent of 8.875.
Understanding the Decimal Representation: Place Value
The decimal 8.875 can be broken down into its place values:
- 8: Represents 8 ones.
- 8: Represents 8 tenths (8/10).
- 7: Represents 7 hundredths (7/100).
- 5: Represents 5 thousandths (5/1000).
This highlights the base-10 system of decimals, where each digit's position determines its value.
Why This Conversion is Important
The ability to convert fractions to decimals is vital in numerous contexts:
- Financial Calculations: Dealing with money often involves fractions of a dollar (cents), which are easily represented as decimals.
- Scientific Measurements: Many scientific measurements utilize decimals for precise representation.
- Engineering and Design: Precise calculations in engineering and design require accurate decimal representations.
- Data Analysis: Data analysis often involves working with decimal numbers for statistical calculations.
- Everyday Life: From calculating tips to measuring ingredients, understanding decimals is essential for daily tasks.
Practical Applications and Examples
Let's consider some scenarios where converting 8 7/8 to its decimal equivalent is useful:
- Measuring Length: If you are measuring a length of 8 7/8 inches, you might need the decimal equivalent (8.875 inches) for precise calculations or compatibility with digital measuring tools.
- Calculating Costs: If an item costs $8 7/8, converting it to $8.875 allows for easier calculations involving multiple items or discounts.
- Averaging Scores: If your average score on a test is 8 7/8 out of 10, expressing this as 8.875 allows for easier comparison with other scores represented as decimals.
Different Methods and Their Suitability
While both methods described above achieve the same result, their suitability may vary depending on the context:
- Method 1 (Direct Decimal Conversion): This method is generally simpler and faster for mixed numbers with relatively easy-to-divide fractions. It's a great approach for beginners.
- Method 2 (Improper Fraction Conversion): This method is more useful when dealing with complex fractions or when a deeper understanding of fractional representation is needed. It reinforces the relationship between fractions and decimals.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted to terminating decimals?
No. Only fractions whose denominators have only 2 and/or 5 as prime factors will result in terminating decimals. Fractions with other prime factors in their denominator will result in repeating decimals (e.g., 1/3 = 0.333...).
Q2: What if the fraction has a larger numerator?
The process remains the same. You would still divide the numerator by the denominator to obtain the decimal equivalent.
Q3: Are there other ways to convert fractions to decimals?
Yes, you can use a calculator or software programs designed for mathematical computations. However, understanding the manual methods is crucial for building a foundational understanding of the concept.
Q4: What if I have a negative mixed number?
The conversion process remains the same. Simply convert the fraction to a decimal, and then keep the negative sign. For example, -8 7/8 would be -8.875.
Conclusion: Mastering Decimal Conversions
Converting 8 7/8 to its decimal equivalent, 8.875, is a fundamental skill with broad applications. Understanding the different methods and the underlying principles allows for more confident and accurate mathematical calculations across various disciplines. While using calculators is convenient, grasping the manual conversion techniques provides a deeper comprehension of the relationship between fractions and decimals, strengthening your mathematical foundation. Remember to practice regularly to build proficiency and confidence in handling these conversions. The ability to confidently navigate between fractions and decimals empowers you to solve problems more efficiently and accurately in various academic and real-world scenarios. This skill serves as a crucial building block for more advanced mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 8 7/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.