7 Out Of 12 Percentage
defexpoindia
Sep 21, 2025 · 5 min read
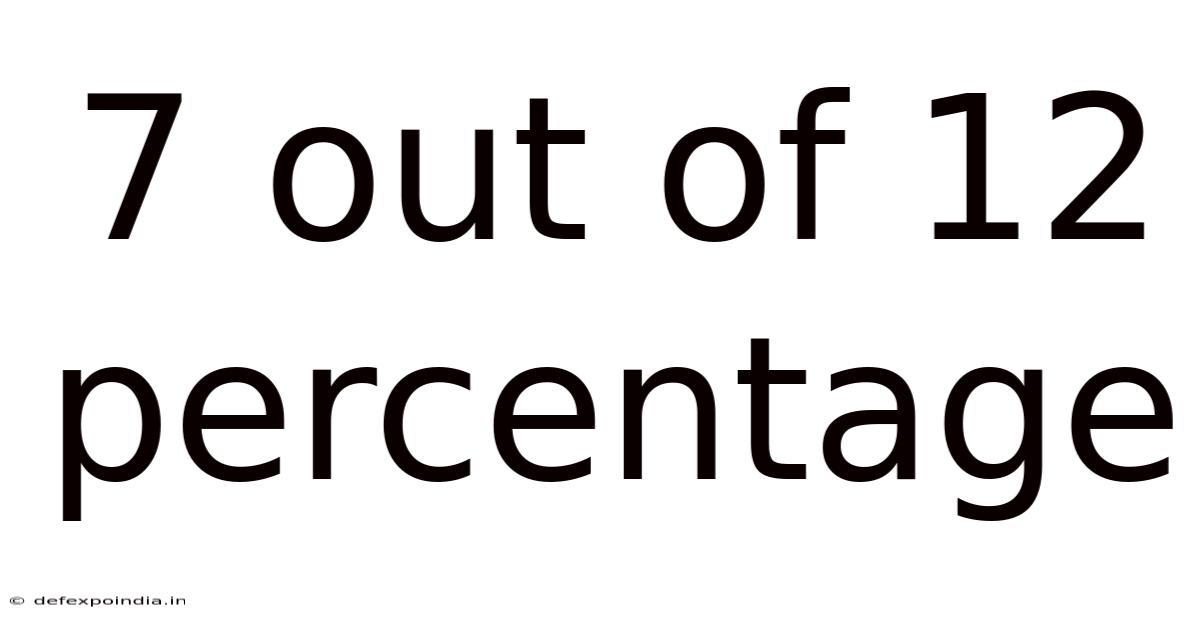
Table of Contents
Decoding 7 out of 12: A Comprehensive Guide to Percentages, Fractions, and Ratios
Understanding percentages is a fundamental skill in everyday life, from calculating discounts to assessing test scores. This article delves deep into the seemingly simple concept of "7 out of 12," exploring its representation as a fraction, decimal, and percentage, and demonstrating its practical applications. We'll also tackle common misconceptions and provide a solid foundation for mastering percentage calculations. This guide is perfect for students, professionals, or anyone looking to strengthen their mathematical understanding.
Introduction: Understanding the Basics
The phrase "7 out of 12" represents a part-to-whole relationship. It signifies that 7 units are selected from a total of 12 units. This concept can be expressed in several ways: as a fraction, a decimal, or a percentage. Each representation offers a different perspective on the same underlying relationship.
-
Fraction: The most direct representation is the fraction 7/12. The numerator (7) represents the part, and the denominator (12) represents the whole.
-
Decimal: To convert the fraction to a decimal, we divide the numerator by the denominator: 7 ÷ 12 ≈ 0.5833.
-
Percentage: To express this as a percentage, we multiply the decimal by 100: 0.5833 × 100 ≈ 58.33%. This means that 7 out of 12 represents approximately 58.33% of the whole.
Steps to Calculate 7 out of 12 as a Percentage
Let's break down the calculation process step-by-step:
-
Form the Fraction: Express "7 out of 12" as the fraction 7/12.
-
Convert to Decimal: Divide the numerator (7) by the denominator (12): 7 ÷ 12 = 0.583333... (The 3s repeat infinitely).
-
Convert to Percentage: Multiply the decimal by 100: 0.583333... × 100 = 58.3333...%
-
Rounding: For practical purposes, we usually round the percentage to a reasonable number of decimal places. Rounding to two decimal places gives us 58.33%.
Visualizing 7 out of 12
Visual aids can significantly improve understanding. Imagine a pizza cut into 12 equal slices. If you eat 7 slices, you've consumed 7/12 of the pizza, which is approximately 58.33% of the whole pizza. This visual representation makes the abstract concept more concrete and easier to grasp. Similarly, you could use a bar graph or a pie chart to visually represent this proportion.
Real-World Applications of 7 out of 12
The concept of "7 out of 12" has numerous real-world applications:
-
Test Scores: If a student answers 7 out of 12 questions correctly on a test, their score is 58.33%.
-
Surveys and Polls: If 7 out of 12 respondents agree with a particular statement in a survey, the agreement rate is 58.33%.
-
Manufacturing and Quality Control: If 7 out of 12 manufactured items are defective, the defect rate is 58.33%.
-
Sports Statistics: In sports, this could represent the success rate of a player in a specific situation (e.g., 7 successful free throws out of 12 attempts).
-
Project Management: If 7 out of 12 tasks in a project are completed, the project completion rate is 58.33%.
Further Exploration: Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is crucial for mastering these concepts. Let's revisit the core principles:
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number).
-
Decimals: Represent a fraction using a base-ten system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
-
Percentages: Represent a fraction or decimal as a proportion of 100. The symbol "%" denotes "per hundred."
Converting between these three representations is a fundamental skill:
- Fraction to Decimal: Divide the numerator by the denominator.
- Decimal to Percentage: Multiply the decimal by 100.
- Percentage to Decimal: Divide the percentage by 100.
- Decimal to Fraction: Write the decimal as a fraction with a power of 10 as the denominator (e.g., 0.5833 can be approximated as 5833/10000). Then, simplify the fraction if possible.
Addressing Common Misconceptions
Several misconceptions surround percentages:
-
Confusing Part and Whole: Clearly identifying the "part" and the "whole" is crucial for accurate calculations.
-
Incorrect Rounding: Rounding percentages appropriately is essential for clear communication.
-
Misunderstanding Percentage Increase/Decrease: Percentage increase or decrease calculations require careful consideration of the initial value.
Advanced Applications: Proportions and Ratios
The concept of "7 out of 12" can be extended to understand proportions and ratios. A ratio compares two quantities, often written as 7:12 or 7/12. A proportion states that two ratios are equal. These concepts are fundamental in various fields, including:
- Scaling: Enlarging or reducing images or objects maintains the same ratio.
- Mixing Ingredients: Recipes often use ratios to specify ingredient quantities.
- Financial Calculations: Ratios are used extensively in financial analysis.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase or decrease?
- A: To calculate a percentage increase, find the difference between the new value and the original value, divide by the original value, and multiply by 100. For a percentage decrease, the process is similar, but the result will be negative.
-
Q: What if I have a different "out of" number?
- A: The same principles apply. Simply form a fraction with the "part" as the numerator and the "whole" as the denominator, convert to a decimal, and then multiply by 100 to get the percentage.
-
Q: How do I deal with repeating decimals when converting fractions to percentages?
- A: You can round the decimal to a reasonable number of decimal places for practical purposes. The level of precision required will depend on the context.
Conclusion: Mastering Percentages for Success
Understanding the concept of "7 out of 12" and its various representations (fraction, decimal, and percentage) is a crucial stepping stone to mastering percentage calculations. This skill is invaluable in many aspects of life, from academic pursuits and professional work to everyday decision-making. By mastering the fundamental principles and practicing regularly, you can build confidence in your ability to handle percentages with ease and accuracy. Remember to always clearly identify the "part" and the "whole" before beginning your calculations, and don't hesitate to use visual aids to aid your understanding. Through consistent practice and a deeper comprehension of the underlying mathematical principles, you can unlock the power of percentages and apply them effectively in various situations.
Latest Posts
Latest Posts
-
How Long Is 100 Centimeters
Sep 21, 2025
-
Convert Lux To Foot Candles
Sep 21, 2025
-
How Many Feet Is 30cm
Sep 21, 2025
-
8 Percent As A Fraction
Sep 21, 2025
-
I 57 M In Feet
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 12 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.