7 1/2 As A Decimal
defexpoindia
Sep 21, 2025 · 5 min read
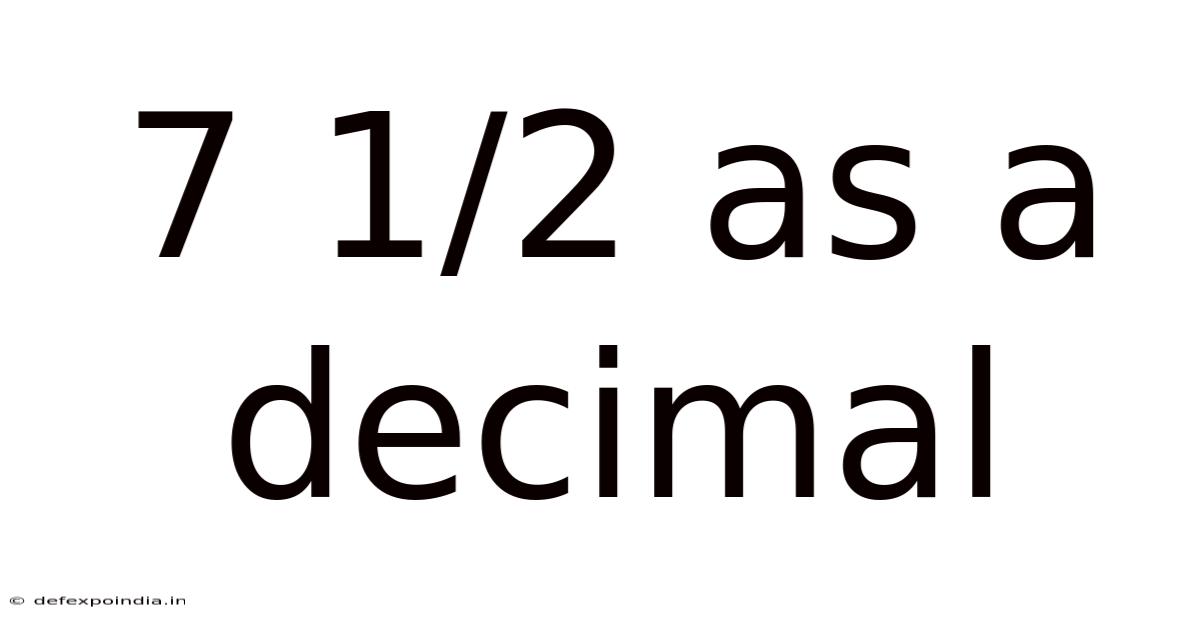
Table of Contents
7 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the mixed number 7 1/2 into its decimal equivalent, explaining the process in detail and addressing common questions. We'll delve into the underlying principles, providing a clear and accessible explanation suitable for learners of all levels. By the end, you'll not only know the answer but also understand the methodology behind it, empowering you to tackle similar conversions with confidence.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's briefly review the concepts of mixed numbers and decimals. A mixed number combines a whole number and a fraction, such as 7 1/2. This represents 7 whole units plus one-half of another unit. A decimal, on the other hand, uses a base-ten system to represent numbers with a fractional part. The decimal point separates the whole number part from the fractional part, with each digit to the right of the decimal representing a decreasing power of ten (tenths, hundredths, thousandths, etc.).
Converting 7 1/2 to a Decimal: Step-by-Step
There are several ways to convert 7 1/2 to a decimal. Here are two common methods:
Method 1: Converting the Fraction to a Decimal and Adding the Whole Number
This method involves converting the fractional part (1/2) into a decimal and then adding it to the whole number (7).
-
Convert the fraction: The fraction 1/2 represents one divided by two. Performing this division, we get 0.5.
-
Add the whole number: Now, add the whole number part (7) to the decimal equivalent of the fraction (0.5): 7 + 0.5 = 7.5
Therefore, 7 1/2 as a decimal is 7.5.
Method 2: Converting the Mixed Number to an Improper Fraction and Then to a Decimal
This method involves first converting the mixed number into an improper fraction and then performing the division to obtain the decimal.
-
Convert to an improper fraction: To convert 7 1/2 to an improper fraction, we multiply the whole number (7) by the denominator of the fraction (2), add the numerator (1), and keep the same denominator (2). This gives us: (7 * 2) + 1 / 2 = 15/2
-
Perform the division: Now, divide the numerator (15) by the denominator (2): 15 ÷ 2 = 7.5
Again, we arrive at the decimal equivalent of 7.5.
Why This Conversion is Important
The ability to convert fractions to decimals is crucial for various reasons:
-
Simplification of Calculations: Decimals often make calculations easier, especially when using calculators or computers. Adding, subtracting, multiplying, and dividing decimals is generally more straightforward than performing the same operations with fractions.
-
Data Representation: Many real-world applications require data to be presented in decimal form. Scientific measurements, financial data, and engineering calculations frequently utilize decimals for precision and clarity.
-
Standardization and Communication: Using decimals provides a common and easily understood format for representing fractional values, facilitating communication and collaboration across different fields and disciplines.
-
Solving Equations: In algebra and other mathematical contexts, the ability to convert between fractions and decimals is often necessary to solve equations and simplify expressions.
Expanding on Decimal Concepts: Place Value and Precision
Understanding place value is vital when working with decimals. In the number 7.5, the '7' represents the ones place, while the '5' represents the tenths place. Each digit to the right of the decimal point has a decreasing value: tenths, hundredths, thousandths, ten-thousandths, and so on. This systematic representation allows for a precise representation of fractional quantities.
The precision of a decimal representation depends on the number of decimal places. 7.5 is precise to one decimal place. If we were dealing with a more complex fraction, we might need more decimal places to accurately represent its value. For instance, 1/3 is approximately 0.33333..., with the '3' repeating infinitely.
Beyond 7 1/2: Converting Other Mixed Numbers to Decimals
The methods described above can be applied to convert any mixed number to a decimal. The key steps are:
-
Separate the whole number and the fraction.
-
Convert the fraction to a decimal by dividing the numerator by the denominator.
-
Add the whole number and the decimal fraction together.
Alternatively, convert the mixed number to an improper fraction and then divide the numerator by the denominator.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 7 1/2 to a decimal?
A: Yes, most calculators have the capability to perform this conversion directly. You can either input "7 + 1/2" or "15/2" to obtain the answer of 7.5.
Q: What if the fraction doesn't divide evenly?
A: If the fraction doesn't divide evenly, you'll get a repeating or terminating decimal. A terminating decimal ends after a finite number of digits (e.g., 1/4 = 0.25). A repeating decimal has a digit or sequence of digits that repeats infinitely (e.g., 1/3 = 0.333...).
Q: How do I convert a decimal back into a fraction?
A: To convert a decimal back into a fraction, you can write the decimal as a fraction over a power of 10. For example, 7.5 can be written as 75/10, which simplifies to 15/2. Then, convert the improper fraction back to a mixed number if needed.
Q: Are there other methods to convert fractions to decimals?
A: Yes, other methods exist, especially for more complex fractions. Long division is a common technique for manually converting fractions to decimals.
Conclusion
Converting 7 1/2 to its decimal equivalent, 7.5, is a straightforward process that utilizes fundamental mathematical concepts. This guide not only provides the answer but also explores the underlying principles of mixed numbers, decimals, place value, and different conversion methods. Understanding these concepts is essential for further mathematical development and for tackling more complex fractional conversions confidently. The ability to seamlessly transition between fractions and decimals is a crucial skill in various academic and practical contexts. Remember that practicing these conversion methods is key to mastering them, so don't hesitate to try converting other mixed numbers on your own!
Latest Posts
Latest Posts
-
5 6 Pies A Centimetros
Sep 21, 2025
-
How Far Is 300 Kilometers
Sep 21, 2025
-
How Much Is 400 Feet
Sep 21, 2025
-
How Tall Is 17 Cm
Sep 21, 2025
-
What Is 174cm In Feet
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.