6 7/8 As A Decimal
defexpoindia
Sep 19, 2025 · 5 min read
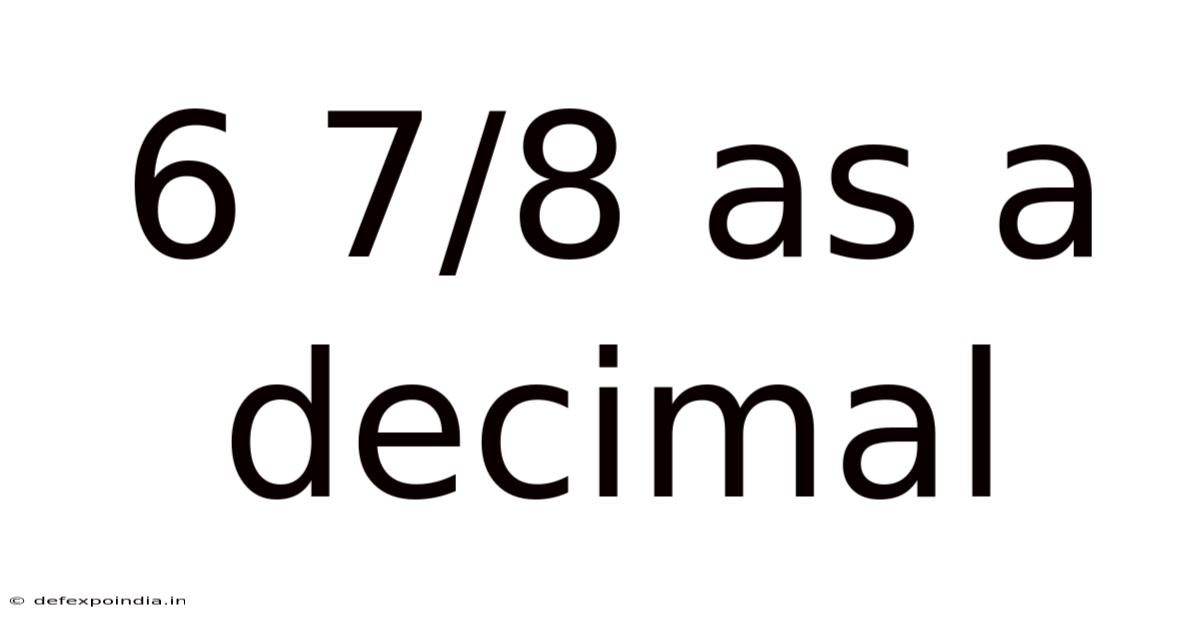
Table of Contents
Understanding 6 7/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article will delve deep into understanding how to convert the mixed number 6 7/8 into its decimal equivalent, exploring the underlying principles and offering multiple approaches to solve this problem. We’ll also address common misconceptions and answer frequently asked questions, ensuring a thorough understanding of this seemingly simple yet important concept.
Understanding Mixed Numbers and Fractions
Before we tackle the conversion, let's briefly review the concepts of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 6 7/8. This signifies six whole units plus seven-eighths of another unit. A fraction, on the other hand, represents a part of a whole. The top number is the numerator (7 in this case), indicating the number of parts we have, and the bottom number is the denominator (8), showing the total number of equal parts the whole is divided into.
To convert a mixed number to a decimal, we need to first convert the mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator. This allows us to represent the entire quantity as a single fractional value.
Converting 6 7/8 to an Improper Fraction
The process of converting 6 7/8 to an improper fraction involves two steps:
- Multiply the whole number by the denominator: 6 * 8 = 48
- Add the numerator to the result: 48 + 7 = 55
This gives us a new numerator of 55. The denominator remains the same (8). Therefore, 6 7/8 is equivalent to the improper fraction 55/8.
Converting the Improper Fraction to a Decimal: Method 1 – Long Division
The most straightforward method to convert 55/8 to a decimal is through long division. We divide the numerator (55) by the denominator (8):
6.875
8 | 55.000
-48
70
-64
60
-56
40
-40
0
As we can see from the long division, 55 divided by 8 equals 6.875. Therefore, 6 7/8 as a decimal is 6.875.
Converting the Improper Fraction to a Decimal: Method 2 – Decimal Equivalents of Common Fractions
Knowing the decimal equivalents of common fractions can significantly speed up the conversion process. For instance, it is helpful to memorize that 1/8 = 0.125. Since 7/8 is seven times 1/8, we can calculate it as:
7 * 0.125 = 0.875
Adding this to the whole number 6, we again arrive at the decimal equivalent of 6.875. This method is efficient for fractions with denominators that are powers of 2 (2, 4, 8, 16, etc.), as their decimal equivalents are relatively easy to remember or quickly calculate.
Understanding the Decimal Place Value
The decimal 6.875 consists of three parts:
- 6: Represents the whole number part.
- 0.8: Represents eight-tenths (8/10).
- 0.07: Represents seven-hundredths (7/100).
- 0.005: Represents five-thousandths (5/1000).
Understanding decimal place value is essential for interpreting the results accurately and for performing further calculations.
Practical Applications of Decimal Conversion
Converting fractions to decimals is crucial in various real-world situations:
- Financial Calculations: Dealing with monetary values often requires converting fractions of a dollar or cent into decimal form for accurate calculations.
- Engineering and Design: Precise measurements and calculations in engineering and design projects necessitate the use of decimal numbers.
- Scientific Measurements: Many scientific measurements utilize decimal numbers to represent data accurately.
- Computer Programming: Many programming languages handle numerical data in decimal format.
- Everyday Calculations: Everyday tasks like calculating percentages, proportions, or sharing quantities might require fraction-to-decimal conversion.
Common Misconceptions and Errors
A common mistake when converting mixed numbers to decimals is to incorrectly convert only the fractional part. Remember to include the whole number in the final decimal representation. Another common error is forgetting to carry over numbers during long division, which can lead to an inaccurate result. Carefully review your work to ensure accuracy.
Frequently Asked Questions (FAQ)
Q1: Can I convert 6 7/8 to a decimal using a calculator?
A1: Yes, most calculators have the functionality to perform this conversion directly. You can either input the fraction as 6 + 7/8 or as the improper fraction 55/8 to obtain the decimal result of 6.875.
Q2: What if the fraction doesn't divide evenly?
A2: If the fraction results in a non-terminating decimal (a decimal that goes on forever without repeating), you can either round the decimal to a certain number of decimal places or express it as a recurring decimal using a bar notation (e.g., 1/3 = 0.3̅).
Q3: Why is understanding decimal conversion important?
A3: Decimal conversion is fundamental to many areas of mathematics and science. It's a skill that makes calculations easier, especially in contexts where dealing with fractions is cumbersome or inefficient. It is also crucial for ensuring accuracy and consistency in various fields.
Q4: Are there other methods to convert fractions to decimals besides long division?
A4: Yes, you can also use a calculator, or if you are working with simple fractions, you may find it quicker to mentally convert using known fractional equivalents.
Conclusion
Converting 6 7/8 to a decimal, resulting in 6.875, is a simple yet fundamental mathematical operation. Understanding the process, from converting the mixed number to an improper fraction to performing the long division or leveraging known fractional equivalents, empowers you to tackle similar problems with confidence. Mastering this skill is essential for success in various academic and practical settings, offering a versatile tool for tackling numerical challenges effectively and accurately. Remember the importance of accuracy and precision throughout the conversion process, and don't hesitate to use multiple methods to verify your answer. The ability to seamlessly transition between fractions and decimals is a hallmark of mathematical proficiency.
Latest Posts
Related Post
Thank you for visiting our website which covers about 6 7/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.