5 6 As A Percent
defexpoindia
Sep 21, 2025 · 5 min read
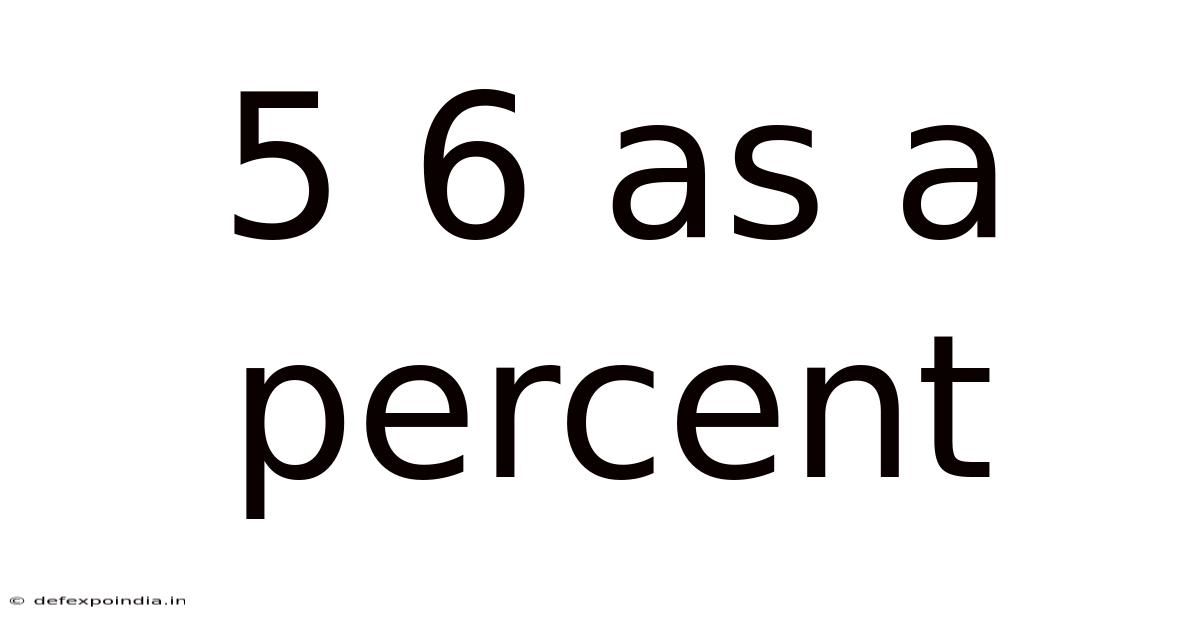
Table of Contents
Understanding 5/6 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 5/6 into a percentage, explaining the steps involved, the underlying principles, and providing practical examples to solidify your understanding. We'll also explore related concepts and answer frequently asked questions to ensure a thorough grasp of this important topic.
Understanding Fractions and Percentages
Before we dive into converting 5/6 to a percentage, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For instance, in the fraction 5/6, 5 is the numerator and 6 is the denominator. This means we have 5 parts out of a possible 6 equal parts.
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Converting 5/6 to a Percentage: Step-by-Step Guide
There are two primary methods to convert 5/6 to a percentage:
Method 1: Using Division
This method involves dividing the numerator by the denominator and then multiplying the result by 100.
-
Divide the numerator by the denominator: 5 ÷ 6 = 0.8333... (The decimal continues infinitely.)
-
Multiply the result by 100: 0.8333... × 100 = 83.33...%
Therefore, 5/6 is approximately 83.33%. The "..." indicates that the decimal is recurring, meaning the '3' repeats infinitely. For practical purposes, we often round to a certain number of decimal places (e.g., 83.33%).
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. This is particularly useful when dealing with fractions that have denominators that are factors of 100 (e.g., 2, 4, 5, 10, 20, 25, 50). While 6 isn't a factor of 100, we can still illustrate the principle with a simpler example before returning to 5/6.
Let's consider the fraction 1/4. To convert this to a percentage, we can find an equivalent fraction with a denominator of 100:
1/4 = (1 × 25) / (4 × 25) = 25/100 = 25%
For 5/6, finding an equivalent fraction with a denominator of 100 isn't straightforward because 6 doesn't divide evenly into 100. However, the method using division, as explained above, remains the most efficient approach.
Understanding the Decimal Representation
The decimal representation of 5/6 (0.8333...) is crucial in understanding the percentage. The decimal represents the portion of the whole that 5/6 constitutes. Multiplying this decimal by 100 simply scales this portion to express it as a percentage – a fraction of 100.
The recurring decimal (0.8333...) highlights that 5/6 cannot be expressed exactly as a finite decimal. This is because the fraction's denominator (6) contains prime factors other than 2 and 5 (specifically, 2 and 3). Only fractions with denominators containing only 2 and 5 as prime factors have terminating decimal representations.
Practical Applications of Converting Fractions to Percentages
The ability to convert fractions to percentages is invaluable in many real-world scenarios:
-
Finance: Calculating interest rates, discounts, and profit margins often involves converting fractions to percentages.
-
Statistics: Representing data in percentage form makes it easier to understand and compare. For instance, if 5 out of 6 students passed an exam, this can be expressed as approximately 83.33% passing rate.
-
Everyday Life: Understanding percentages helps in comparing prices, calculating tips, and interpreting various statistics presented in media and reports.
Rounding and Precision
When working with repeating decimals, like the one we encountered with 5/6, it's essential to decide on an appropriate level of precision. Rounding to two decimal places (83.33%) is often sufficient for most practical purposes. However, for more precise calculations, you might need to use more decimal places or work with the fraction directly.
Frequently Asked Questions (FAQs)
Q1: Why do we multiply by 100 when converting a fraction to a percentage?
A1: We multiply by 100 because a percentage is defined as a fraction out of 100. Multiplying by 100 scales the fraction to express it as a part of 100, thus giving us the percentage.
Q2: Can all fractions be converted to percentages?
A2: Yes, all fractions can be converted to percentages. The process involves dividing the numerator by the denominator and then multiplying by 100.
Q3: What if I get a very long decimal when converting a fraction?
A3: If you get a very long or repeating decimal, it's acceptable to round the result to a suitable number of decimal places for practical purposes. The level of precision needed depends on the context of the problem.
Q4: Is there a way to convert percentages back to fractions?
A4: Yes, to convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 83.33% can be converted back to 5/6 (approximately, due to rounding).
Q5: Are there any online calculators that can help with this conversion?
A5: Yes, many online calculators are readily available to convert fractions to percentages and vice versa. However, understanding the underlying process is crucial for broader mathematical comprehension.
Conclusion
Converting 5/6 to a percentage involves a straightforward process of dividing the numerator by the denominator and multiplying the result by 100. This yields approximately 83.33%. Understanding this conversion is crucial for various applications in mathematics and real-world situations. Remember to consider the level of precision needed when rounding decimals, especially when dealing with repeating decimals. The ability to confidently convert fractions to percentages demonstrates a solid grasp of fundamental mathematical principles, empowering you to tackle more complex numerical problems with ease. This guide aimed to provide a comprehensive understanding of the process, equipping you with the knowledge and skills to confidently handle such conversions in the future.
Latest Posts
Latest Posts
-
21x 30 Cm In Inches
Sep 21, 2025
-
How Many Feet Is 58
Sep 21, 2025
-
300 Meters In Square Feet
Sep 21, 2025
-
How Much Is Two Meters
Sep 21, 2025
-
How Long Is 70 Millimeters
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 5 6 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.