5 5/8 As A Decimal
defexpoindia
Sep 13, 2025 · 5 min read
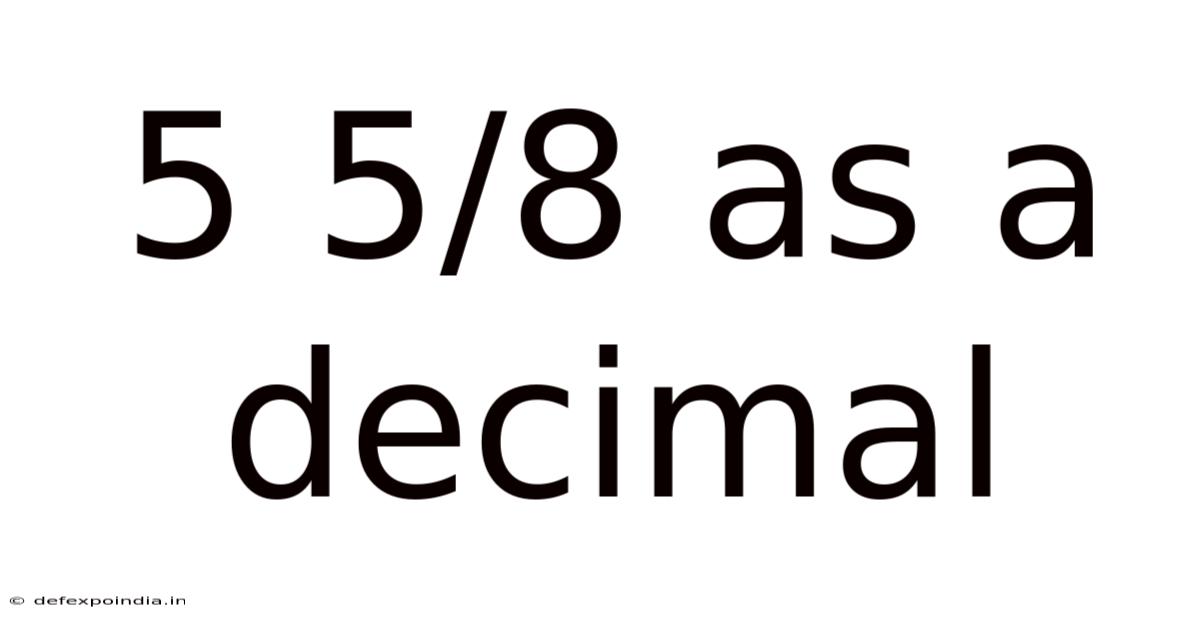
Table of Contents
5 5/8 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 5 5/8 into its decimal equivalent. We'll cover the process step-by-step, explore the underlying mathematical principles, and even delve into some practical applications. This guide is designed for learners of all levels, from those just starting to grasp fractions to those seeking a deeper understanding of decimal representation. By the end, you'll not only know the answer but also understand why the conversion works.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's clarify some key terms. A mixed number combines a whole number and a fraction, like 5 5/8. The whole number (5 in this case) represents complete units, while the fraction (5/8) represents a portion of a unit. A fraction, in its simplest form, represents a part of a whole. The top number is called the numerator (5 in 5/8) and the bottom number is the denominator (8 in 5/8). The denominator indicates how many equal parts the whole is divided into.
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This is the most straightforward approach for converting 5 5/8 to a decimal. We'll first focus on converting the fraction 5/8 to a decimal, and then add the whole number 5.
Step 1: Divide the Numerator by the Denominator
To convert a fraction to a decimal, you simply divide the numerator by the denominator. In this case, we divide 5 by 8:
5 ÷ 8 = 0.625
Step 2: Add the Whole Number
Now that we have the decimal equivalent of the fraction (0.625), we add the whole number part of the mixed number:
5 + 0.625 = 5.625
Therefore, 5 5/8 as a decimal is 5.625.
Method 2: Converting the Mixed Number to an Improper Fraction First
An alternative method involves first converting the mixed number into an improper fraction, and then converting the improper fraction to a decimal. This method is useful for understanding the underlying mathematical relationships.
Step 1: Convert to an Improper Fraction
To convert a mixed number to an improper fraction, we multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator remains the same.
(5 × 8) + 5 = 45
So, 5 5/8 becomes 45/8.
Step 2: Divide the Numerator by the Denominator
Now, we divide the numerator (45) by the denominator (8):
45 ÷ 8 = 5.625
Again, we arrive at the same answer: 5 5/8 as a decimal is 5.625.
Method 3: Using Decimal Equivalents of Common Fractions
For those familiar with common fraction-to-decimal conversions, you might recognize that 1/8 = 0.125. Since 5/8 is five times 1/8, we can simply multiply 0.125 by 5:
0.125 × 5 = 0.625
Then, add the whole number 5:
5 + 0.625 = 5.625
This method is quicker once you’ve memorized the decimal equivalents of common fractions like 1/2, 1/4, 1/8, 1/10, etc.
Understanding the Decimal Representation: Place Value
The decimal number 5.625 represents 5 units, 6 tenths, 2 hundredths, and 5 thousandths. Understanding place value is crucial for interpreting decimal numbers accurately. Each digit to the right of the decimal point represents a decreasing power of 10.
Practical Applications of Decimal Conversions
Converting fractions to decimals is essential in many real-world situations:
- Financial Calculations: Dealing with money often involves decimal values. For example, calculating interest rates or splitting bills.
- Measurements: Many measurements, such as lengths, weights, and volumes, use decimal units (e.g., centimeters, kilograms, liters). Converting fractions to decimals ensures consistency in calculations.
- Data Analysis: In statistics and data analysis, fractions are often converted to decimals for easier interpretation and computation.
- Engineering and Design: Precise calculations in engineering and design frequently require the use of decimal numbers.
- Computer Programming: Computers work with binary numbers, which are easily converted to and from decimal representations.
Further Exploration: Recurring Decimals
While 5 5/8 converts to a terminating decimal (a decimal that ends), not all fractions do. Some fractions, when converted to decimals, result in recurring decimals – decimals that repeat a sequence of digits infinitely. For example, 1/3 = 0.3333... (the 3s repeat indefinitely). Understanding the difference between terminating and recurring decimals is important for advanced mathematical work.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to convert 5 5/8 to a decimal?
- A: Yes, absolutely. Most calculators have a division function that can easily handle this conversion. Simply divide 5 by 8 and add 5 to the result.
-
Q: What if the fraction has a larger numerator than denominator?
- A: If the numerator is larger than the denominator, the resulting decimal will be greater than 1. For example, 9/8 = 1.125. You would still use the same division method.
-
Q: Is there a way to convert decimals back to fractions?
- A: Yes, there is. The process involves identifying the place value of the last digit in the decimal and using that as the denominator of the fraction. The numerator is the number itself without the decimal point. Then, simplify the fraction to its lowest terms if possible. For example, 0.625 can be expressed as 625/1000, which simplifies to 5/8.
-
Q: Why is understanding this conversion important?
- A: This conversion is a crucial building block in mathematics and its applications. It bridges the gap between fractional and decimal representations, enabling seamless calculations across various fields.
Conclusion
Converting 5 5/8 to a decimal is a straightforward process, achievable through several methods. Understanding the underlying principles of fractions, decimals, and the different conversion methods is key to mastering this fundamental mathematical skill. Whether you use division directly, convert to an improper fraction first, or leverage your knowledge of common fraction-to-decimal equivalents, the result remains the same: 5 5/8 is equal to 5.625. Mastering this skill will enhance your mathematical abilities and improve your proficiency in various real-world applications. Remember to practice regularly to build confidence and fluency in converting fractions to decimals. This foundational knowledge will serve you well in future mathematical endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 5/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.