5 3/8 As A Decimal
defexpoindia
Sep 23, 2025 · 5 min read
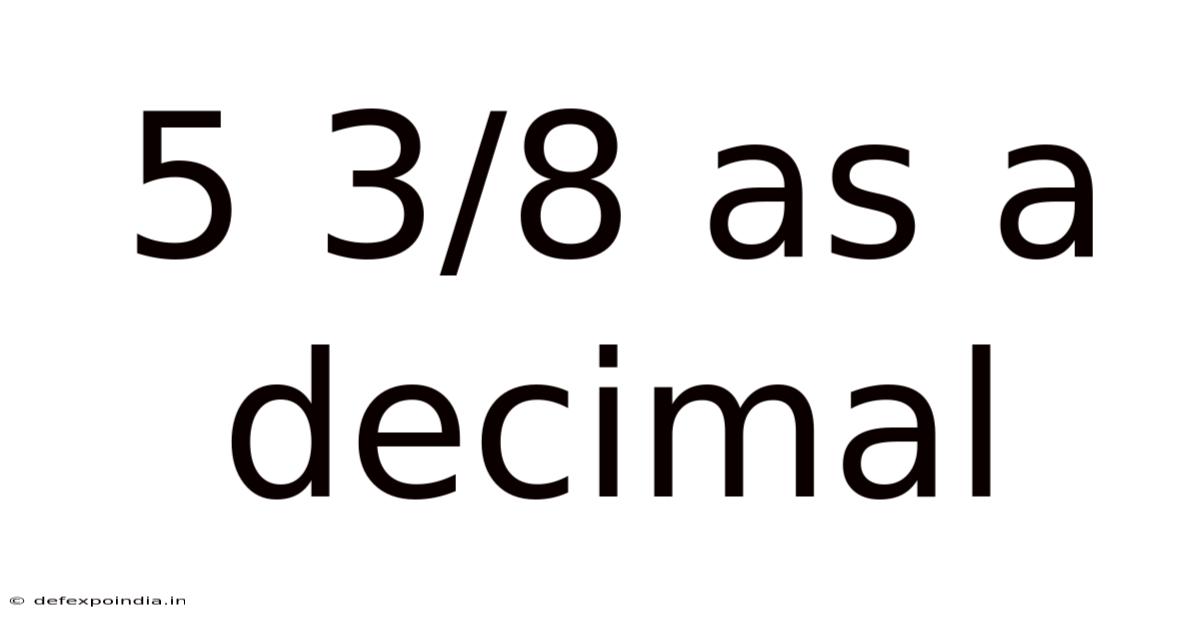
Table of Contents
5 3/8 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. This comprehensive guide will walk you through the process of converting the mixed number 5 3/8 into its decimal equivalent, explaining the underlying principles and offering practical examples. We'll explore different methods, address common misconceptions, and delve into the practical significance of this conversion. This guide is designed for students, educators, and anyone seeking a deeper understanding of decimal representation.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's refresh our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 5 3/8. This represents 5 whole units plus 3/8 of another unit. A fraction, such as 3/8, indicates a part of a whole, where the top number (3, the numerator) represents the number of parts, and the bottom number (8, the denominator) represents the total number of equal parts the whole is divided into.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is perhaps the most straightforward method. We'll first convert the fractional part (3/8) into a decimal, and then add the whole number (5).
-
Divide the numerator by the denominator: To convert 3/8 to a decimal, we perform the division 3 ÷ 8. This results in 0.375.
-
Add the whole number: Now, add the whole number 5 to the decimal value we obtained: 5 + 0.375 = 5.375
Therefore, 5 3/8 as a decimal is 5.375.
Method 2: Converting the Entire Mixed Number into an Improper Fraction, Then to a Decimal
This method involves transforming the mixed number into an improper fraction—a fraction where the numerator is larger than or equal to the denominator—before converting it to a decimal.
-
Convert to an improper fraction: To convert 5 3/8 to an improper fraction, we multiply the whole number (5) by the denominator (8), add the numerator (3), and keep the same denominator (8). This gives us: (5 * 8) + 3 = 43. The improper fraction is 43/8.
-
Divide the numerator by the denominator: Now, divide the numerator (43) by the denominator (8): 43 ÷ 8 = 5.375
Again, we arrive at the decimal equivalent of 5.375.
Method 3: Using Long Division (for a deeper understanding)
This method offers a more visual representation of the division process and is helpful for understanding the underlying mechanics. While less efficient for simple fractions, it's valuable for grasping the concept.
-
Set up the long division: Write 8 (the denominator) outside the division symbol and 3 (the numerator) inside. Since we're dealing with a mixed number, remember the whole number 5 will be added later.
-
Perform the long division: You'll find that 8 goes into 3 zero times, so you add a decimal point and a zero to the 3, making it 30. 8 goes into 30 three times (8 x 3 = 24), leaving a remainder of 6. Add another zero and bring down the 6, making it 60. 8 goes into 60 seven times (8 x 7 = 56), leaving a remainder of 4. Add another zero, making it 40. 8 goes into 40 five times (8 x 5 = 40), leaving no remainder.
-
Combine the results: This gives us 0.375. Now add the whole number 5 to get 5.375.
Why Understanding Decimal Equivalents is Important
The ability to convert fractions to decimals is essential for several reasons:
-
Calculations: Decimals are often easier to work with in calculations, especially when using calculators or computers. Adding, subtracting, multiplying, and dividing decimals are generally simpler than performing the same operations with fractions.
-
Comparisons: Comparing fractions can be challenging, but comparing decimals is straightforward. For example, determining which is larger, 5 3/8 or 5.4, is much easier when both numbers are expressed as decimals (5.375 and 5.4).
-
Real-world applications: Many real-world measurements and quantities are expressed as decimals (e.g., weight, length, volume, currency). Understanding decimal equivalents allows us to seamlessly integrate fractional values into practical applications.
-
Scientific and engineering fields: Decimals are crucial in scientific notation and various engineering calculations, providing a standardized and precise way to represent quantities.
Addressing Common Misconceptions
A common mistake is to simply divide the numerator by the whole number. Remember, you always divide the numerator by the denominator.
Another misconception is assuming that all fractions have finite decimal representations. Some fractions, like 1/3 (which equals 0.333…), result in repeating decimals. However, 3/8 has a terminating decimal (a decimal that ends), which is 0.375.
Frequently Asked Questions (FAQs)
-
Q: Can I convert any fraction to a decimal? A: Yes, any fraction can be converted to a decimal by dividing the numerator by the denominator. However, the resulting decimal may be terminating (ending) or repeating (continuing indefinitely).
-
Q: What if the decimal representation is very long? A: For very long or repeating decimals, you can round the decimal to a suitable number of decimal places depending on the required level of accuracy.
-
Q: Are there any shortcuts for converting specific fractions to decimals? A: Yes, some common fractions, like 1/2 (0.5), 1/4 (0.25), and 1/8 (0.125), are frequently encountered and easily memorized. This knowledge can expedite calculations.
-
Q: How do I convert a decimal back into a fraction? A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (e.g., 10, 100, 1000). Then, simplify the fraction to its lowest terms. For example, 0.375 can be written as 375/1000, which simplifies to 3/8.
Conclusion:
Converting 5 3/8 to its decimal equivalent, 5.375, involves a straightforward process that can be approached through several methods. This conversion, as illustrated, is a fundamental skill with broad practical applications. Understanding these methods not only enhances mathematical proficiency but also equips individuals with essential tools for various quantitative tasks across various fields. Remember to choose the method that best suits your understanding and the complexity of the fraction you are working with. Mastering this skill will undoubtedly contribute to a more confident and efficient approach to numerical problem-solving.
Latest Posts
Latest Posts
-
How Heavy Is 2 Kilograms
Sep 23, 2025
-
34 Degrees C In Fahrenheit
Sep 23, 2025
-
2 O6 M In Feet
Sep 23, 2025
-
78 Degrees F To C
Sep 23, 2025
-
Convert 160 Cm To Inch
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 3/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.