5 3/4 In Decimal Form
defexpoindia
Sep 20, 2025 · 5 min read
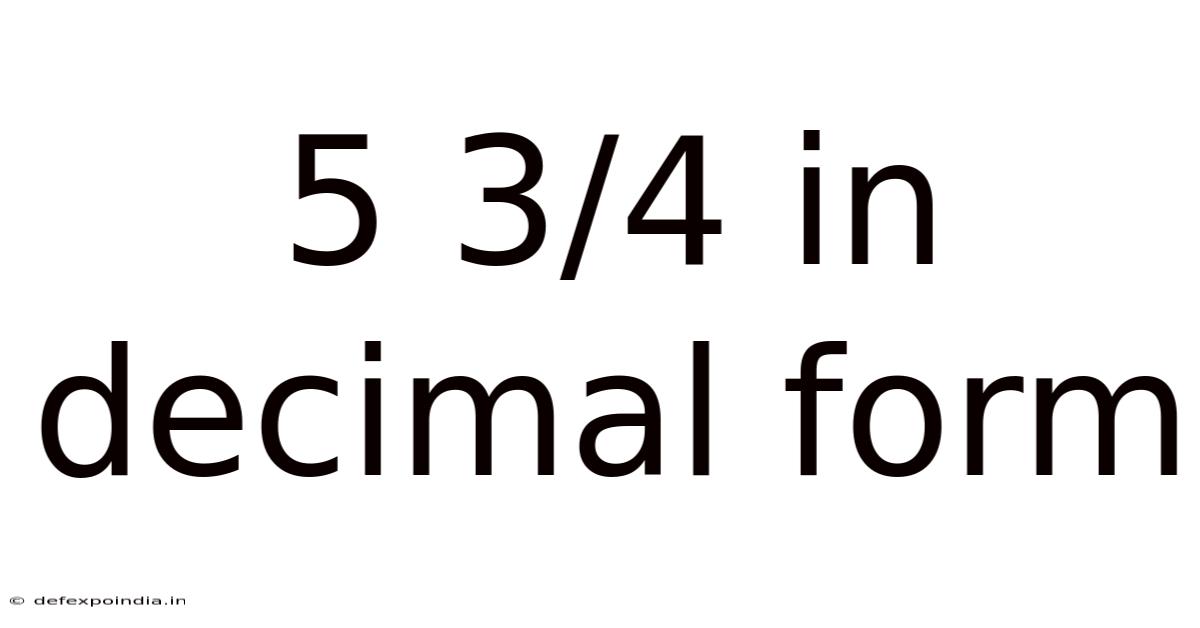
Table of Contents
Decoding 5 3/4: A Deep Dive into Decimal Conversion and its Applications
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, essential for various fields from everyday calculations to advanced scientific applications. This article focuses on converting the mixed number 5 3/4 into its decimal equivalent. We'll explore the process in detail, explain the underlying mathematical principles, delve into practical applications, and address frequently asked questions. This comprehensive guide aims to provide a clear and thorough understanding of this seemingly simple yet crucial concept.
Introduction: Why Decimal Conversion Matters
The ability to convert fractions like 5 3/4 into decimal form (5.75) is vital for several reasons. Decimals offer a standardized and easily comparable format for numbers. They are especially crucial when dealing with calculations involving percentages, monetary values, measurements (especially in the metric system), and data analysis. Understanding this conversion process facilitates seamless transitions between fractional and decimal representations, enhancing mathematical fluency and problem-solving skills.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's solidify our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, such as 5 3/4. This represents 5 whole units plus an additional 3/4 of a unit. The fraction 3/4 is comprised of a numerator (3) and a denominator (4). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts that make up a whole.
Converting 5 3/4 to Decimal Form: Step-by-Step Guide
There are two primary methods to convert 5 3/4 to its decimal equivalent. Both methods lead to the same answer, but one might be more intuitive depending on your mathematical background.
Method 1: Converting the Fraction First
-
Focus on the Fraction: First, we address the fractional part, 3/4. This means we need to find out what portion of 1 is represented by 3 out of 4 equal parts.
-
Divide the Numerator by the Denominator: To convert a fraction to a decimal, we divide the numerator by the denominator. In this case, we perform the division 3 ÷ 4 = 0.75.
-
Combine with the Whole Number: Now, we combine the resulting decimal (0.75) with the whole number (5). This gives us the final decimal representation: 5.75.
Therefore, 5 3/4 is equal to 5.75 in decimal form.
Method 2: Converting to an Improper Fraction First
-
Convert to an Improper Fraction: A mixed number can be transformed into an improper fraction, where the numerator is larger than the denominator. To do this, we multiply the whole number by the denominator and add the numerator. In our example: (5 x 4) + 3 = 23. This becomes the new numerator, while the denominator remains the same (4). So, 5 3/4 becomes 23/4.
-
Divide the Numerator by the Denominator: Next, we divide the numerator (23) by the denominator (4): 23 ÷ 4 = 5.75.
Again, we arrive at the decimal equivalent: 5.75.
Mathematical Principles Underlying the Conversion
The conversion from a fraction to a decimal fundamentally involves the concept of division. A fraction inherently represents a division operation; the numerator is divided by the denominator. When we perform this division, the result is the decimal representation of the fraction. This is based on the fundamental principle that any fraction can be expressed as a decimal, either as a terminating decimal (like 0.75) or a repeating decimal (like 1/3 = 0.333...).
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals has wide-ranging applications across various fields:
-
Finance: Calculating monetary values, percentages (like discounts or interest rates), and managing budgets all heavily rely on decimal representation. For example, understanding that 5 3/4 dollars is equal to $5.75 is crucial for accurate financial calculations.
-
Measurements: In the metric system, measurements are primarily expressed using decimals. Converting fractional measurements to decimal form is necessary for consistent and precise calculations. Imagine working with blueprints; precise decimal measurements are indispensable.
-
Data Analysis: Data analysis frequently involves calculations and comparisons of numerical data. Representing data in a consistent decimal format simplifies calculations and allows for efficient data manipulation and interpretation.
-
Science and Engineering: Scientific and engineering calculations require high precision. Converting fractions to decimals ensures accuracy in calculations involving distances, weights, volumes, and other physical quantities.
-
Cooking and Baking: Recipes often include fractional measurements of ingredients. Converting these fractions to decimals can simplify the measuring process, especially when using digital scales.
Frequently Asked Questions (FAQs)
Q1: Can all fractions be converted to terminating decimals?
No. Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals. For instance, 1/3 = 0.333... However, fractions with denominators that are only divisible by 2 and/or 5 will always result in terminating decimals.
Q2: What if I have a larger mixed number? Does the process change?
No, the process remains the same. You simply focus on converting the fractional part to a decimal and then combine it with the whole number.
Q3: Are there any online calculators that can help with this conversion?
Yes, many online calculators are available to perform fraction-to-decimal conversions. These tools can be helpful for verification or for larger, more complex fractions.
Q4: What is the significance of understanding this concept?
Mastering fraction-to-decimal conversion is essential for building a strong foundation in mathematics. It enhances computational skills and opens doors to more advanced mathematical concepts.
Conclusion: Mastering a Fundamental Skill
Converting 5 3/4 to its decimal equivalent (5.75) is more than just a simple mathematical operation; it represents the mastery of a fundamental skill vital for numerous applications. By understanding the underlying principles and the various methods of conversion, you equip yourself with a powerful tool for navigating various mathematical and real-world scenarios. The seemingly straightforward conversion process underscores the interconnectedness of different mathematical representations and highlights the importance of numerical fluency in tackling everyday challenges and advancing in various fields. The ability to seamlessly transition between fractions and decimals is a testament to a strong mathematical foundation.
Latest Posts
Latest Posts
-
1 Horse Power To Kw
Sep 20, 2025
-
How Tall Is 91 Cm
Sep 20, 2025
-
Lux Conversion To Foot Candles
Sep 20, 2025
-
Watt To Joules Per Second
Sep 20, 2025
-
100 900 Meters To Kilometers
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 5 3/4 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.