40 Percent Of 1 Million
defexpoindia
Sep 23, 2025 · 6 min read
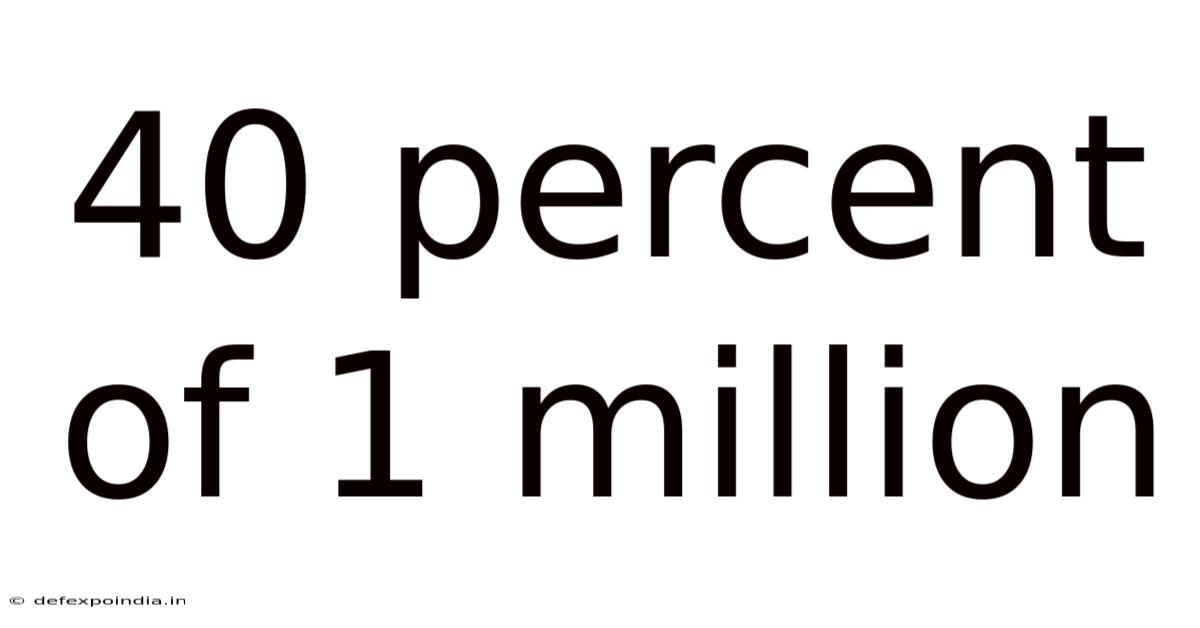
Table of Contents
Decoding 40% of 1 Million: A Comprehensive Guide
Finding 40% of 1 million might seem like a simple arithmetic problem, but understanding the underlying concepts can open doors to broader applications in various fields, from finance and business to everyday life calculations. This comprehensive guide will not only show you how to calculate 40% of 1 million but also delve into the methodology, explore practical applications, and address frequently asked questions. This will equip you with a strong understanding of percentages and their real-world relevance.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 40% means 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40.
Calculating 40% of 1 Million: The Methods
There are several ways to calculate 40% of 1 million. Let's explore the most common and straightforward approaches:
Method 1: Using Decimal Multiplication
This is arguably the most efficient method. We convert the percentage to its decimal equivalent and then multiply it by the total value.
- Step 1: Convert 40% to a decimal: 40% = 40/100 = 0.40
- Step 2: Multiply the decimal by 1,000,000: 0.40 * 1,000,000 = 400,000
Therefore, 40% of 1 million is $\boxed{400,000}$.
Method 2: Using Fraction Multiplication
This method involves expressing the percentage as a fraction and then performing the multiplication.
- Step 1: Express 40% as a fraction: 40% = 40/100
- Step 2: Simplify the fraction: 40/100 simplifies to 2/5
- Step 3: Multiply the fraction by 1,000,000: (2/5) * 1,000,000 = 2 * (1,000,000/5) = 2 * 200,000 = 400,000
Again, we arrive at the answer: 40% of 1 million is $\boxed{400,000}$.
Method 3: Proportional Reasoning
This method utilizes the concept of ratios and proportions. We can set up a proportion to solve for the unknown value.
- Step 1: Set up a proportion: 40/100 = x/1,000,000, where 'x' represents 40% of 1 million.
- Step 2: Cross-multiply: 40 * 1,000,000 = 100 * x
- Step 3: Solve for x: 40,000,000 = 100x => x = 40,000,000 / 100 = 400,000
This confirms that 40% of 1 million is $\boxed{400,000}$.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples:
-
Finance: Calculating interest earned on savings accounts, determining discounts on purchases, understanding tax rates, analyzing investment returns, and assessing loan repayments all involve percentage calculations. For example, if you have a savings account with a 4% annual interest rate and a balance of $1 million, your annual interest would be 4% of $1 million, or $40,000.
-
Business: Businesses use percentage calculations extensively in profit margin analysis, sales growth tracking, market share determination, and pricing strategies. A company's profit margin, for instance, is often expressed as a percentage of revenue. If a company has a profit margin of 20% and a revenue of 1 million dollars, the profit would be 20% of 1 million, or 200,000 dollars.
-
Data Analysis: Percentages are fundamental to expressing data in a concise and easily understandable manner. In data analysis and reporting, percentages are invaluable for comparing and contrasting different data sets. Imagine a survey with 1 million respondents; percentages can effectively represent the distribution of responses amongst different categories.
-
Everyday Life: From calculating tips in restaurants (e.g., a 20% tip on a $50 meal) to understanding discounts in stores (e.g., a 15% off sale), percentage calculations are integral to our daily financial decision-making.
Beyond the Basics: Working with Different Percentages and Values
The methods outlined above can be applied to calculate any percentage of any value. For example, to find 25% of 500,000, you would convert 25% to its decimal equivalent (0.25) and then multiply it by 500,000 (0.25 * 500,000 = 125,000). This adaptable approach allows for wide-ranging calculations. Similarly, if you need to find what percentage a given number represents of another, you can use the same proportion method.
Advanced Concepts: Compound Interest and Percentage Change
The concept of percentages extends beyond simple calculations. Two important advanced concepts include:
-
Compound Interest: This involves earning interest not only on the principal amount but also on the accumulated interest. Over time, compound interest can significantly increase the overall value of an investment. The formula for compound interest is: A = P (1 + r/n)^(nt), where A is the future value of the investment/loan, including interest, P is the principal investment amount (the initial deposit or loan amount), r is the annual interest rate (decimal), n is the number of times that interest is compounded per year, and t is the number of years the money is invested or borrowed for.
-
Percentage Change: This measures the relative change between two values. It's calculated as [(New Value - Old Value) / Old Value] * 100%. For example, if a company's revenue increased from $500,000 to $600,000, the percentage change would be [(600,000 - 500,000) / 500,000] * 100% = 20%. This shows a 20% increase in revenue.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a different percentage of 1 million?
A1: Follow the same methods outlined above, simply substituting the desired percentage. For example, to calculate 15% of 1 million:
- Convert 15% to a decimal: 15/100 = 0.15
- Multiply the decimal by 1,000,000: 0.15 * 1,000,000 = 150,000
Q2: What if I need to find the percentage one number represents of another?
A2: Use proportional reasoning. Let's say you want to find what percentage 300,000 represents of 1 million:
- Set up a proportion: x/100 = 300,000/1,000,000
- Cross-multiply: 1,000,000x = 30,000,000
- Solve for x: x = 30,000,000/1,000,000 = 30 Therefore, 300,000 represents 30% of 1 million.
Q3: Can I use a calculator for these calculations?
A3: Absolutely! Calculators can greatly simplify these calculations, especially with larger numbers. Most calculators have a percentage function (%) that can directly calculate percentages.
Q4: Are there any online calculators available for percentage calculations?
A4: Yes, many free online calculators are readily available that can assist with various percentage-based calculations.
Conclusion
Calculating 40% of 1 million, while seemingly straightforward, provides a valuable foundation for understanding and applying percentage calculations across numerous disciplines. Mastering these techniques empowers you to confidently tackle various financial, business, and everyday challenges that involve percentages. By understanding the different methods and their applications, you gain a powerful tool for analyzing data, making informed decisions, and effectively navigating the quantitative aspects of the world around you. Remember that the key lies in understanding the underlying concepts, and with practice, these calculations will become second nature.
Latest Posts
Latest Posts
-
How Much Is 500 Kg
Sep 23, 2025
-
800g To Lbs And Oz
Sep 23, 2025
-
3 5 Oz Convert To Grams
Sep 23, 2025
-
1 3 In In Cm
Sep 23, 2025
-
800g Of Chicken To Lbs
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 40 Percent Of 1 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.