3 Out Of 6 Percentage
defexpoindia
Sep 21, 2025 · 6 min read
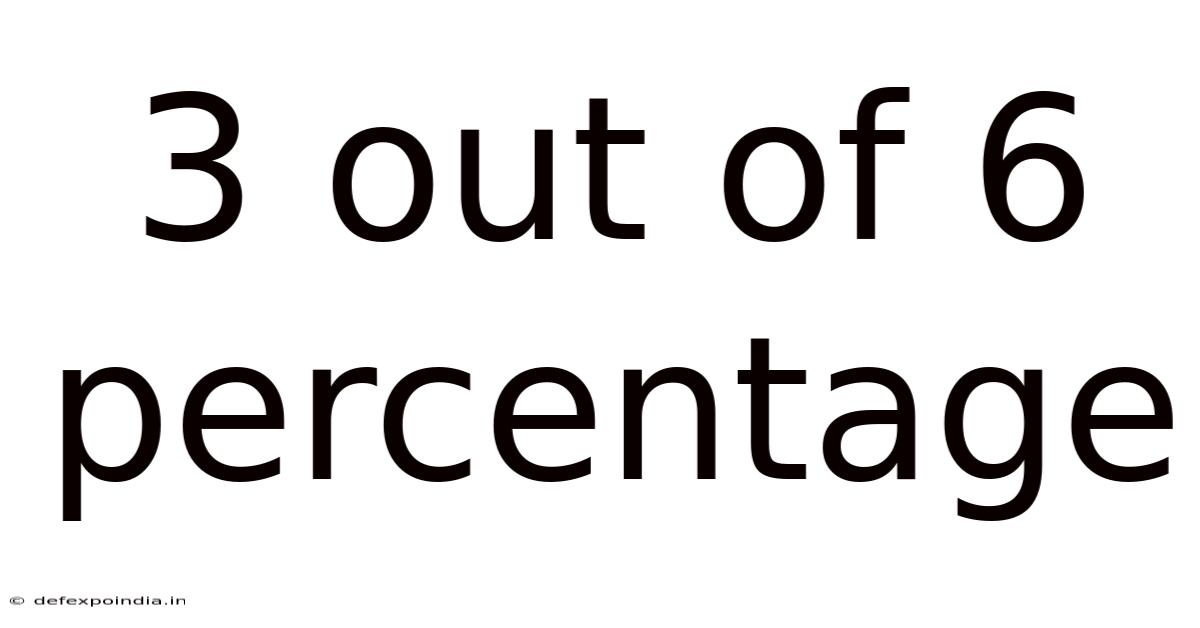
Table of Contents
Understanding 3 out of 6: Percentages, Fractions, and Real-World Applications
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts in a store to comprehending complex statistical data. This article delves into the seemingly simple concept of "3 out of 6," explaining how to express it as a fraction, a decimal, and most importantly, a percentage. We will explore different methods of calculation, address common misconceptions, and provide real-world examples to solidify your understanding. This comprehensive guide is designed for learners of all levels, from those just beginning to understand fractions to those seeking to reinforce their grasp of percentage calculations.
Introduction: Deconstructing "3 out of 6"
The phrase "3 out of 6" represents a ratio. It indicates that 3 items possess a certain characteristic out of a total of 6 items. This ratio can be expressed in various ways, each with its own advantages depending on the context. We'll explore the conversion to fractions, decimals, and ultimately, percentages, revealing the underlying mathematical principles involved. Understanding these conversions is crucial for accurately interpreting and applying this information in various scenarios.
Expressing 3 out of 6 as a Fraction
The most straightforward way to represent "3 out of 6" is as a fraction. A fraction represents a part of a whole. In this case, 3 is the part, and 6 is the whole. Therefore, we write this as:
3/6
This fraction can be simplified by finding the greatest common divisor (GCD) of both the numerator (3) and the denominator (6). The GCD of 3 and 6 is 3. Dividing both the numerator and the denominator by 3, we get:
1/2
This simplified fraction, 1/2, is equivalent to 3/6 and represents the same proportion. It is often easier to work with simplified fractions, especially when comparing ratios or performing further calculations.
Converting the Fraction to a Decimal
To convert the fraction 1/2 (or 3/6) to a decimal, we simply divide the numerator by the denominator:
1 ÷ 2 = 0.5
Therefore, "3 out of 6" is equivalent to 0.5 as a decimal. Decimals are useful for calculations, especially when working with computers or calculators. They provide a concise numerical representation of the ratio.
Calculating the Percentage: The Key to Understanding 3 out of 6
The most common way to express a ratio is as a percentage. A percentage is a fraction expressed as a number out of 100. To convert the fraction 1/2 (or the decimal 0.5) to a percentage, we multiply by 100%:
(1/2) * 100% = 50%
Alternatively, using the decimal:
0.5 * 100% = 50%
Therefore, "3 out of 6" represents 50%. This percentage clearly communicates that half (50%) of the total items possess the specified characteristic.
Different Methods for Calculating Percentages
While the above method is straightforward, there are alternative approaches to calculating percentages. Understanding these alternative methods can enhance your problem-solving skills and help you choose the most efficient approach for a given situation.
-
Using Proportions: We can set up a proportion:
3/6 = x/100
Solving for x (the percentage) involves cross-multiplication:
6x = 300
x = 50
Therefore, x = 50%, confirming our previous result.
-
Using the Decimal Method Directly: Starting with the original ratio 3/6, we can directly convert it to a decimal (0.5) and then multiply by 100% to obtain the percentage (50%). This method eliminates the need for fraction simplification.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the conversion process. Simply input 3/6 and then press the percentage button to directly obtain 50%.
Real-World Applications of Understanding 3 out of 6 (50%)
The concept of "3 out of 6," or 50%, has wide-ranging applications in various real-world scenarios:
-
Academic Performance: If a student answers 3 out of 6 questions correctly on a quiz, their score is 50%. This allows for easy assessment of performance.
-
Sales and Discounts: A store offering a 50% discount means you pay half the original price. Understanding percentages allows you to quickly calculate the final price.
-
Statistical Analysis: In surveys or experiments, 50% represents a significant proportion. It indicates a clear trend or preference.
-
Probability and Odds: In simple probability scenarios, a 50% chance means an equal likelihood of an event occurring or not occurring (like flipping a coin).
-
Financial Calculations: Understanding percentages is essential for calculating interest rates, loan repayments, and investment returns.
Addressing Common Misconceptions
Several common misconceptions surround percentage calculations. Let's clarify some of them:
-
Incorrect Simplification: Failing to simplify fractions before converting to percentages can lead to inaccurate results. Always simplify the fraction to its lowest terms before proceeding.
-
Misplacing the Decimal Point: Errors in decimal placement during conversion can significantly affect the final percentage. Double-check your work to avoid these errors.
-
Confusing Percentages with Fractions: While related, percentages and fractions represent different forms of expressing proportions. Understanding the conversion between them is crucial.
-
Overlooking the "Whole": Accurately identifying the "whole" (the denominator) is essential for correct percentage calculation. Misidentifying the whole leads to incorrect results.
Frequently Asked Questions (FAQ)
-
Q: Can I calculate the percentage directly from the ratio without converting to a fraction or decimal?
A: While less common, you can. You could use the proportion method directly from the ratio 3/6, setting up the proportion 3/6 = x/100 and solving for x.
-
Q: What if the numbers are larger, such as 30 out of 60?
A: The principle remains the same. 30/60 simplifies to 1/2, which is still 50%. Larger numbers might require a calculator for efficient calculation, but the underlying concept doesn't change.
-
Q: How do I calculate percentages for numbers that don't easily simplify?
A: For ratios that don't simplify easily, directly converting the fraction to a decimal and then multiplying by 100% is generally the most efficient method. A calculator can be very helpful in these situations.
-
Q: Are there any online tools or calculators to help with percentage calculations?
A: Many online calculators and tools are available to assist with percentage calculations. These can be useful for checking your work or for more complex percentage problems.
Conclusion: Mastering the Art of Percentages
Understanding "3 out of 6" as a percentage—50%—is a fundamental skill with broad applications. By mastering the techniques explained in this article, you'll be better equipped to handle percentage calculations in various contexts. Remember to focus on correctly identifying the "whole," simplifying fractions, and avoiding common errors in decimal placement. Consistent practice and a clear understanding of the underlying principles will solidify your understanding and improve your ability to confidently work with percentages in your daily life, academic pursuits, and professional endeavors. The seemingly simple concept of "3 out of 6" opens the door to a world of quantitative reasoning and problem-solving.
Latest Posts
Latest Posts
-
3 5 In Decimal Form
Sep 21, 2025
-
42 9 As A Decimal
Sep 21, 2025
-
What Is Half A Kg
Sep 21, 2025
-
How Much Is Ten Miles
Sep 21, 2025
-
63 Po Farengeytu V Tselsiyakh
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 6 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.