3/8 Percent As A Decimal
defexpoindia
Sep 19, 2025 · 5 min read
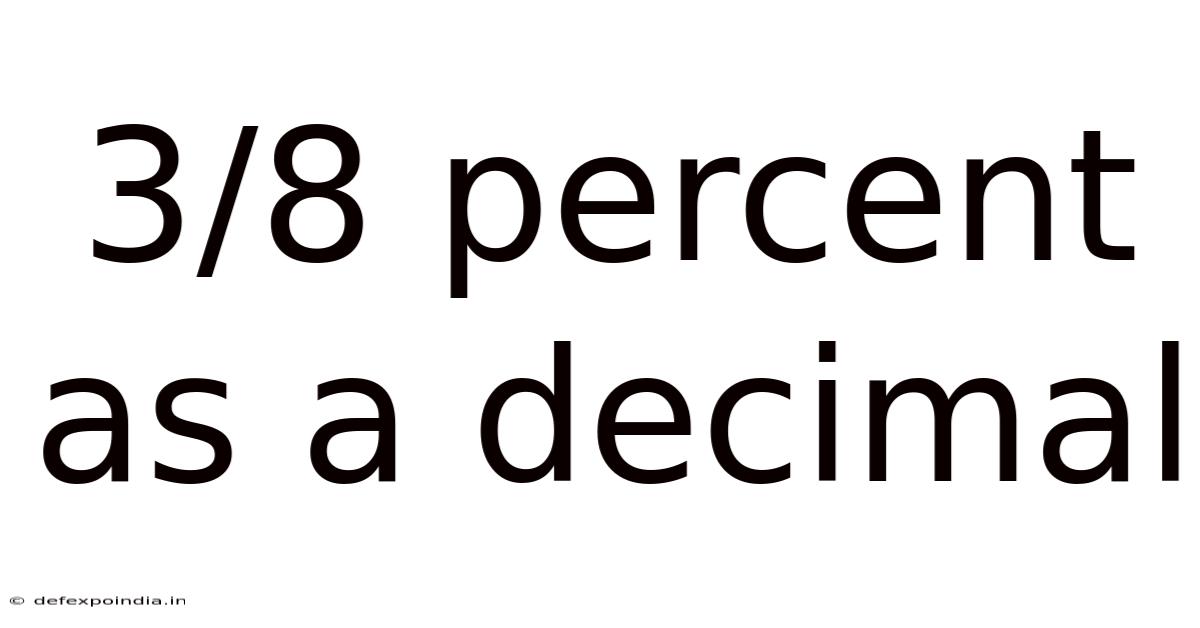
Table of Contents
Understanding 3/8 Percent as a Decimal: A Comprehensive Guide
Converting fractions and percentages to decimals is a fundamental skill in mathematics with applications spanning various fields, from finance and engineering to everyday calculations. This article will provide a thorough explanation of how to convert 3/8 percent into its decimal equivalent, covering the underlying principles and offering practical examples to solidify your understanding. We'll explore different methods, address common misconceptions, and delve into the significance of understanding decimal representation in real-world scenarios.
Introduction: Decimals, Fractions, and Percentages – The Interconnected Trio
Before diving into the specific conversion of 3/8 percent, let's establish a clear understanding of the relationship between decimals, fractions, and percentages. These three forms represent proportions or parts of a whole, but they use different notations.
-
Fractions: Express parts of a whole using a numerator (top number) and a denominator (bottom number). For example, 3/8 represents three out of eight equal parts.
-
Percentages: Represent parts of a whole as a fraction of 100. The symbol "%" signifies "per hundred". For example, 25% means 25 out of 100, or 25/100.
-
Decimals: Express parts of a whole using a base-ten system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For example, 0.25 represents twenty-five hundredths.
These three systems are interchangeable. Understanding their relationships allows for easy conversion between them.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
The most straightforward approach to converting 3/8 percent to a decimal involves a two-step process:
-
Convert the fraction to a decimal: To convert 3/8 to a decimal, we divide the numerator (3) by the denominator (8):
3 ÷ 8 = 0.375
-
Convert the decimal to a percentage: Remember that a percentage is a fraction out of 100. To convert a decimal to a percentage, multiply by 100 and add the "%" symbol:
0.375 x 100 = 37.5%
Therefore, 3/8 as a percentage is 37.5%. However, the original problem states "3/8 percent," meaning we need to take another step. Since "percent" implies "per hundred," 3/8 percent is actually (3/8)/100.
-
Convert 3/8 percent to a decimal: Now we need to convert 37.5% to a decimal. We divide the percentage by 100:
37.5 ÷ 100 = 0.375
Therefore, 3/8 percent as a decimal is 0.00375.
Method 2: Direct Conversion from Fraction to Decimal (for 3/8 percent)
We can also tackle this problem directly, by understanding that 3/8 percent represents (3/8)/100. This can be written as a complex fraction:
(3/8) / 100
To simplify this, we can rewrite 100 as 100/1:
(3/8) / (100/1)
To divide fractions, we invert the second fraction and multiply:
(3/8) * (1/100) = 3/800
Now, we can convert the fraction 3/800 to a decimal by dividing 3 by 800:
3 ÷ 800 = 0.00375
This method confirms our previous result: 3/8 percent as a decimal is 0.00375.
Method 3: Using Proportions
Another approach is to use proportions. We know that 3/8 percent is equivalent to x/100 (where x is the decimal we want to find). Therefore, we set up a proportion:
(3/8)/100 = x/1
This can be simplified as:
3/800 = x
Solving for x:
x = 3 ÷ 800 = 0.00375
Again, this confirms our result.
The Significance of Understanding Decimal Representation
Understanding decimal representation is crucial for several reasons:
-
Calculations: Decimals facilitate calculations, especially when working with percentages, proportions, and financial applications. They are more readily used in calculators and computer programs than fractions.
-
Comparisons: Comparing values is easier with decimals. For example, comparing 0.00375 and 0.01 is straightforward. It would be more difficult to compare 3/800 and 1/100 directly.
-
Precision: Decimals allow for greater precision. Expressing values to several decimal places can significantly increase the accuracy of measurements and calculations, especially in scientific and engineering fields.
Common Misconceptions
A common mistake is to directly convert 3/8 to a decimal (0.375) and then assume this is the answer for 3/8 percent. This neglects the fact that we're dealing with percent, a fraction of 100.
Frequently Asked Questions (FAQ)
-
Q: What if I have a larger fraction, such as 15/32 percent?
A: Follow the same process: convert the fraction to a decimal (15/32 = 0.46875), then convert that decimal to a percentage (0.46875 x 100 = 46.875%), and finally convert that percentage to a decimal (46.875/100 = 0.0046875).
-
Q: Why is it important to distinguish between 3/8 and 3/8 percent?
A: 3/8 represents a larger proportion (37.5%) than 3/8 percent (0.375%). Failing to distinguish between these leads to incorrect calculations and significantly different results. The inclusion of “percent” makes a huge difference to the final value.
-
Q: Are there other methods to convert fractions to decimals?
A: Yes, you can sometimes convert fractions to equivalent fractions with a denominator that's a power of 10 (e.g., 10, 100, 1000). However, this method isn't always practical for all fractions. Division remains the most reliable and general method.
Conclusion:
Converting 3/8 percent to its decimal equivalent – 0.00375 – involves a clear understanding of the relationships between fractions, decimals, and percentages. By following the steps outlined above, using either direct conversion or the method of converting first to percentage then to decimal, anyone can confidently perform this type of conversion. Mastery of this skill significantly enhances one's ability to work with proportions, percentages, and numerical calculations across various disciplines. Remembering the crucial distinction between, for example, 3/8 and 3/8 percent is vital to preventing calculation errors. Always carefully consider the context and units involved.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3/8 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.