3 5/8 As A Decimal
defexpoindia
Sep 21, 2025 · 5 min read
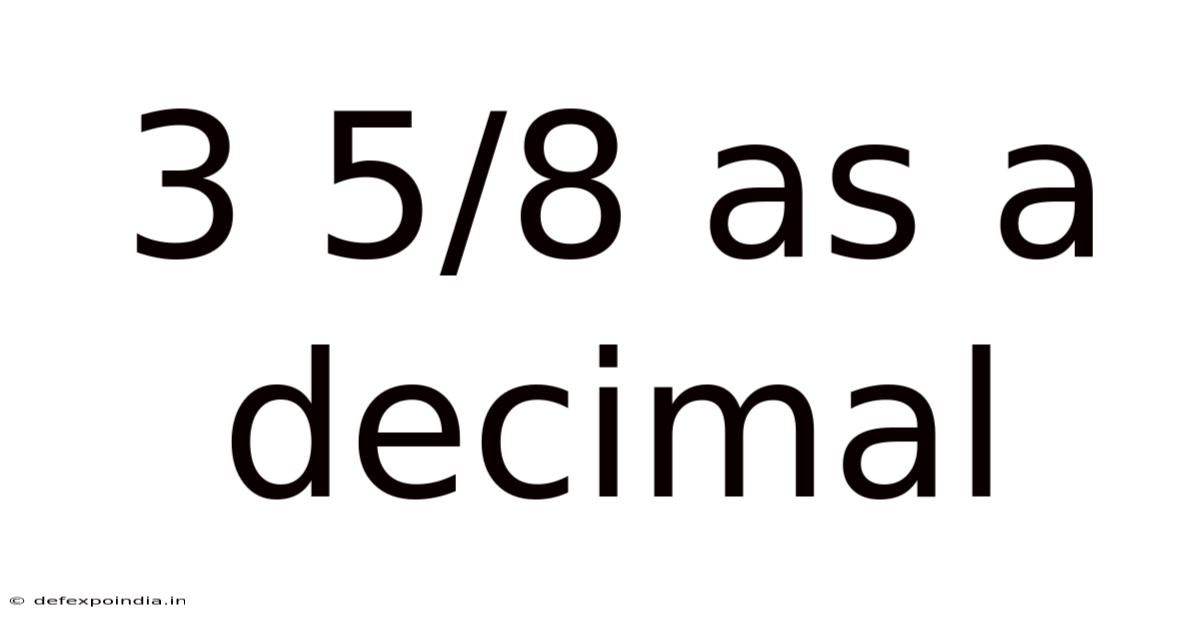
Table of Contents
Understanding 3 5/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will walk you through the process of converting the mixed number 3 5/8 into its decimal equivalent, explaining the underlying principles and providing practical examples. We'll explore different methods, delve into the underlying mathematical concepts, and answer frequently asked questions. This detailed explanation will equip you with a solid understanding of this common conversion, solidifying your foundation in numerical operations.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 3 5/8. This represents 3 whole units plus 5/8 of another unit. A fraction, on the other hand, represents a part of a whole. In 5/8, 5 is the numerator (the number of parts we have) and 8 is the denominator (the total number of equal parts the whole is divided into).
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is perhaps the most straightforward method. We first convert the fractional part (5/8) into a decimal and then add the whole number (3).
Step 1: Divide the numerator by the denominator.
To convert 5/8 to a decimal, we perform the division 5 ÷ 8. This gives us 0.625.
Step 2: Add the whole number.
Now, we add the whole number part (3) to the decimal equivalent of the fraction (0.625): 3 + 0.625 = 3.625
Therefore, 3 5/8 as a decimal is 3.625.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves transforming the mixed number into an improper fraction first. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
Step 1: Convert the mixed number to an improper fraction.
To do this, we multiply the whole number by the denominator and add the numerator. The result becomes the new numerator, while the denominator remains the same.
(3 × 8) + 5 = 29
So, 3 5/8 becomes 29/8.
Step 2: Divide the numerator by the denominator.
Now, we divide the numerator (29) by the denominator (8): 29 ÷ 8 = 3.625
Therefore, 3 5/8 as a decimal is 3.625. This confirms the result we obtained using the first method.
Method 3: Using Decimal Equivalents of Common Fractions
For those familiar with common fraction-to-decimal conversions, you might recognize that 1/8 = 0.125. Since 5/8 is five times 1/8, we can simply multiply 0.125 by 5:
0.125 × 5 = 0.625
Adding the whole number 3, we get 3.625.
This method is faster if you already know the decimal equivalent of the fractional part. Memorizing decimal equivalents for common fractions like 1/2, 1/4, 1/8, 1/10, etc., can significantly speed up your calculations.
The Mathematical Principle Behind the Conversion
The core principle behind converting fractions to decimals lies in the understanding that a fraction represents division. The fraction a/b is equivalent to a ÷ b. When we divide the numerator by the denominator, we are essentially expressing the fractional part as a number of tenths, hundredths, thousandths, and so on – the decimal system.
Practical Applications of Decimal Conversion
Converting fractions to decimals is a vital skill across many fields:
- Finance: Calculating interest rates, discounts, and profit margins often requires converting fractions to decimals.
- Engineering: Precise measurements and calculations in design and construction rely on decimal accuracy.
- Science: Scientific data is often expressed in decimal form, requiring conversion from fractions if the initial data is in fractional form.
- Cooking and Baking: Recipes often use fractional measurements, which need to be converted to decimal equivalents for precise measuring using digital scales.
- Everyday Life: Calculating tips, splitting bills, and understanding percentages all involve working with decimals.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a decimal?
A1: Yes, you can convert any fraction to a decimal by dividing the numerator by the denominator. However, some fractions will result in terminating decimals (like 3.625), while others will result in repeating decimals (like 1/3 = 0.3333...).
Q2: What if the fraction has a very large denominator?
A2: For fractions with large denominators, a calculator is highly recommended to avoid errors in manual division. Long division can become tedious and prone to mistakes with large numbers.
Q3: Is there a way to quickly convert fractions to decimals without a calculator?
A3: Memorizing the decimal equivalents of common fractions can significantly speed up the process. Also, understanding how to simplify fractions before converting can make the division easier.
Q4: What if the mixed number involves a negative fraction?
A4: Treat the conversion as you would with a positive fraction. After converting the fraction to a decimal, simply add the negative sign to the resulting decimal. For example, -3 5/8 would be calculated as -3.625.
Q5: Are there any online tools or calculators that can perform this conversion?
A5: While there are several online tools and calculators available for this conversion, performing the calculation manually helps reinforce understanding of the underlying mathematical principles. However, using calculators is recommended for large numbers or complex fractions to save time and ensure accuracy.
Conclusion
Converting 3 5/8 to its decimal equivalent (3.625) is a straightforward process achievable through various methods. Understanding the underlying mathematical principles—that fractions represent division—is key. By mastering this conversion, you solidify your understanding of fractions and decimals, essential skills for various mathematical applications in both academic and real-world scenarios. The choice of method depends on your comfort level and the tools available, but the ultimate goal is to arrive at the accurate decimal representation of the mixed number. Regular practice and familiarity with different approaches will improve your speed and accuracy in solving similar problems.
Latest Posts
Latest Posts
-
How Tall Is 17 Cm
Sep 21, 2025
-
What Is 174cm In Feet
Sep 21, 2025
-
Convert 27 Kilos To Pounds
Sep 21, 2025
-
What Is 9 Degrees Celsius
Sep 21, 2025
-
What Percent Is 7 8
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 5/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.