3 1/8 As A Decimal
defexpoindia
Sep 22, 2025 · 5 min read
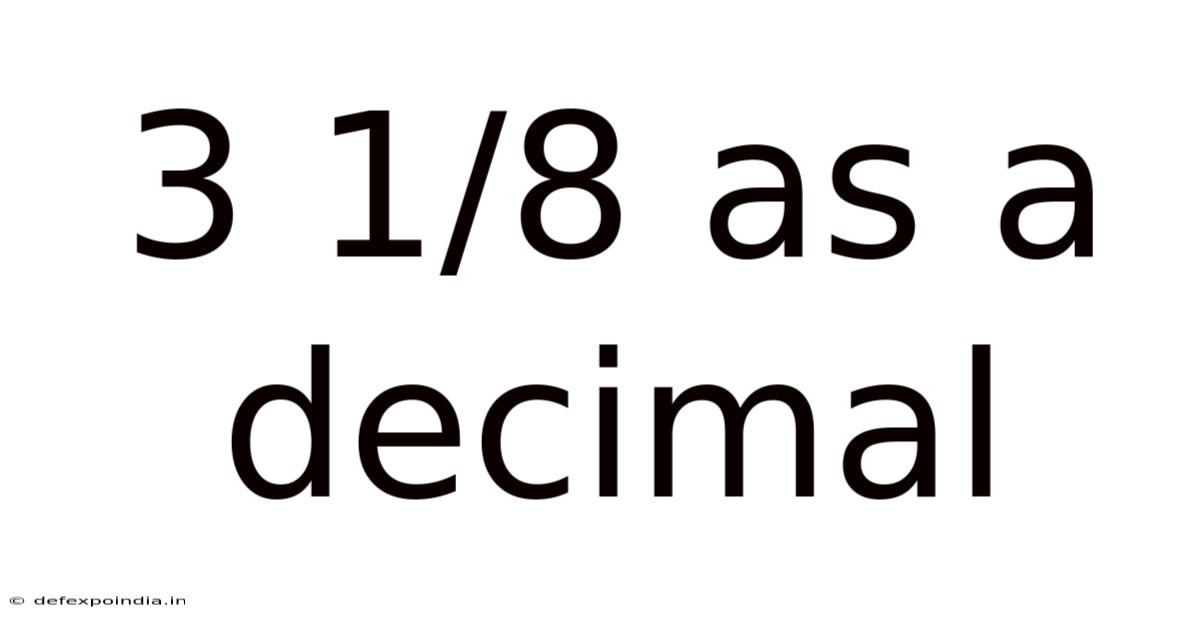
Table of Contents
Understanding 3 1/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the mixed number 3 1/8 into its decimal equivalent, explaining the methodology in detail and providing a deeper understanding of the underlying principles. We'll cover various approaches, address common misconceptions, and even explore some real-world applications.
Understanding Mixed Numbers and Fractions
Before we begin converting 3 1/8 to a decimal, let's refresh our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 3 1/8. This represents 3 whole units plus an additional 1/8 of a unit. A fraction, on the other hand, represents a part of a whole, with the numerator (top number) indicating the number of parts and the denominator (bottom number) indicating the total number of parts that make up the whole.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is perhaps the most straightforward method. We'll first convert the fractional part (1/8) to a decimal and then add the whole number (3).
-
Divide the numerator by the denominator: To convert 1/8 to a decimal, we simply divide the numerator (1) by the denominator (8): 1 ÷ 8 = 0.125
-
Add the whole number: Now, add the whole number part (3) to the decimal equivalent of the fraction: 3 + 0.125 = 3.125
Therefore, 3 1/8 as a decimal is 3.125.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves first converting the mixed number into an improper fraction and then converting that improper fraction to a decimal. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
-
Convert to an improper fraction: To convert 3 1/8 to an improper fraction, we multiply the whole number (3) by the denominator (8), add the numerator (1), and keep the same denominator (8): (3 * 8) + 1 = 25. So, the improper fraction is 25/8.
-
Divide the numerator by the denominator: Now, divide the numerator (25) by the denominator (8): 25 ÷ 8 = 3.125
Again, we arrive at the decimal equivalent of 3.125.
Method 3: Using Long Division (for a deeper understanding)
While the previous methods are quicker, using long division provides a deeper understanding of the conversion process. Let's demonstrate this with 3 1/8:
First, we convert the mixed number to an improper fraction (25/8, as shown in Method 2). Then, we perform long division:
3.125
8 | 25.000
-24
10
-8
20
-16
40
-40
0
The result of the long division is 3.125. This method explicitly shows how the fractional part is represented as a decimal expansion.
Understanding Decimal Places and Significance
The decimal representation of 3 1/8 is 3.125. This number has three decimal places. The first digit after the decimal point (1) represents tenths, the second (2) represents hundredths, and the third (5) represents thousandths. The number can also be expressed as 3 and 125 thousandths. The significance of these decimal places depends on the context of the problem. In some cases, rounding to fewer decimal places might be appropriate (e.g., rounding to 3.12 for simplicity), while in others, all three decimal places are essential for accuracy.
Real-World Applications of Decimal Conversions
Converting fractions to decimals is a practical skill used in many real-world scenarios:
-
Measurements: Imagine measuring ingredients for a recipe. A recipe might call for 3 1/8 cups of flour. Converting this to 3.125 cups makes precise measurement easier.
-
Finance: Calculating interest rates, discounts, and profit margins often involves working with fractions and decimals.
-
Engineering and Science: Precision is crucial in engineering and scientific fields. Converting fractions to decimals ensures accuracy in calculations and measurements.
-
Data Analysis: In statistics and data analysis, working with decimals is more convenient for many calculations and data representations.
-
Computer Programming: Many programming languages require decimal representation for numerical calculations.
Common Mistakes and How to Avoid Them
-
Incorrectly converting to an improper fraction: Ensure you correctly multiply the whole number by the denominator and add the numerator when converting a mixed number to an improper fraction.
-
Division errors: Double-check your division when converting a fraction to a decimal, particularly when dealing with larger numbers or repeating decimals.
-
Rounding errors: Be aware of the level of precision required and round appropriately. Avoid unnecessary rounding that might lead to inaccuracies.
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be converted to terminating decimals?
- A: No. Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals (e.g., 1/3 = 0.333...).
-
Q: What if I have a fraction with a larger numerator and denominator?
- A: The methods described above still apply. Use long division or a calculator for larger numbers.
-
Q: How do I convert a repeating decimal back to a fraction?
- A: This involves setting up an equation and solving for the fraction. This is a more advanced topic, often covered in algebra.
-
Q: Are there online tools to help with fraction-to-decimal conversions?
- A: Yes, many online calculators and converters are available for this purpose. However, understanding the underlying process is crucial for mathematical fluency.
Conclusion
Converting 3 1/8 to a decimal, yielding 3.125, is a straightforward process that involves understanding the relationship between fractions and decimals. Whether you use the direct division method, the improper fraction method, or long division, the result remains the same. Mastering this conversion is essential for various mathematical applications and real-world problems. This comprehensive guide has provided not only the solution but also a deeper understanding of the underlying mathematical principles and practical implications of this fundamental conversion. Remember to practice regularly to build proficiency and confidence in your mathematical skills. The more you work with fractions and decimals, the more intuitive the process will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 1/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.