3 1/2 In Decimal Form
defexpoindia
Sep 23, 2025 · 6 min read
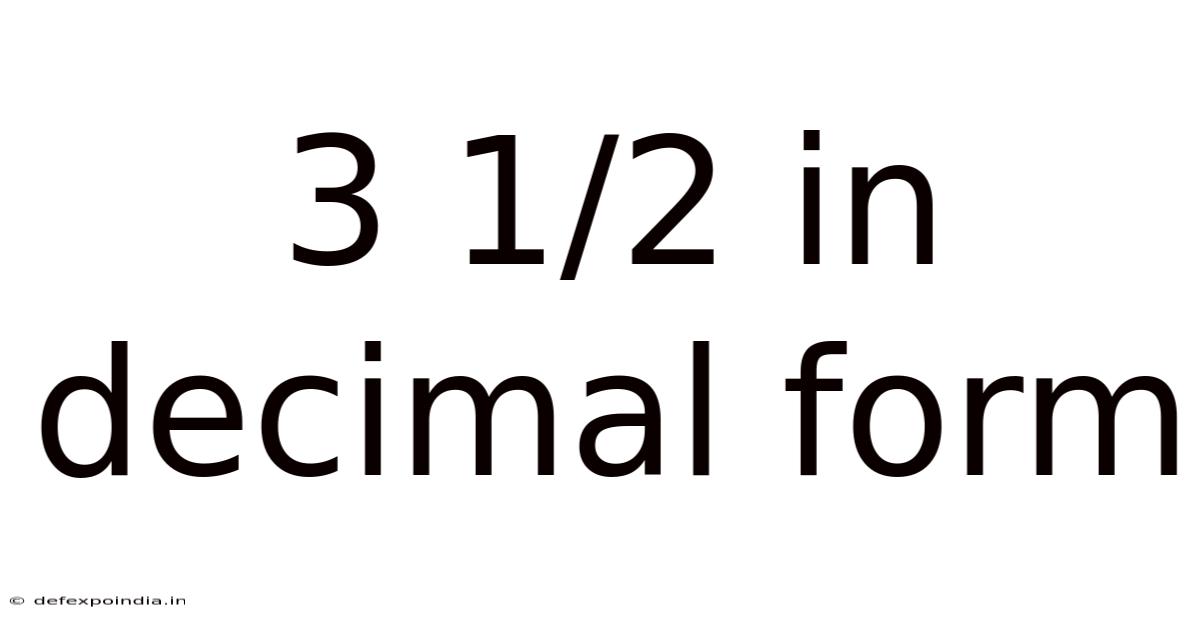
Table of Contents
Understanding 3 1/2 in Decimal Form: A Comprehensive Guide
Mixed numbers, like 3 1/2, are a common part of everyday mathematics. Understanding how to convert them into decimal form is a fundamental skill crucial for various applications, from calculating grocery bills to tackling more complex scientific problems. This article provides a comprehensive guide on converting 3 1/2 to its decimal equivalent, exploring the underlying principles and offering practical examples to solidify your understanding. We'll also delve into the broader context of fractions and decimals, exploring their relationship and providing resources for further learning.
Introduction to Fractions and Decimals
Before diving into the conversion of 3 1/2, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number), separated by a line. The numerator indicates the number of parts you have, and the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2, representing one out of two equal parts.
A decimal, on the other hand, is a number expressed in base-10, using a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.5 represents five tenths, or 5/10.
Converting 3 1/2 to Decimal Form: A Step-by-Step Guide
The mixed number 3 1/2 consists of a whole number part (3) and a fractional part (1/2). To convert this to a decimal, we need to convert the fractional part into its decimal equivalent and then add it to the whole number part.
Here's a step-by-step approach:
-
Convert the fraction to a decimal: The fraction 1/2 means one divided by two. Performing this division gives us 0.5.
-
Add the whole number: Now, add the whole number part (3) to the decimal equivalent of the fraction (0.5). This gives us 3 + 0.5 = 3.5
Therefore, 3 1/2 in decimal form is 3.5.
Alternative Methods for Conversion
While the above method is straightforward, let's explore alternative approaches to reinforce the understanding of fraction-to-decimal conversion.
-
Using Equivalent Fractions: We can convert the fraction 1/2 into an equivalent fraction with a denominator that is a power of 10. Since 2 x 5 = 10, we multiply both the numerator and denominator by 5: (1 x 5) / (2 x 5) = 5/10. 5/10 is equivalent to 0.5, leading to the same result: 3 + 0.5 = 3.5. This method highlights the relationship between fractions and decimals by emphasizing equivalent representations.
-
Long Division: A more fundamental approach involves performing long division. Divide the numerator (1) by the denominator (2). This will yield 0.5. Then add the whole number part (3), resulting in 3.5. This method emphasizes the operational definition of a fraction as a division problem.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is essential in various real-world scenarios:
-
Financial Calculations: Calculating percentages, discounts, interest rates, and splitting bills often requires converting fractions to decimals for easy calculations. For instance, a 1/2 off sale is equivalent to a 0.5 or 50% discount.
-
Measurement and Units: Many measurement systems use both fractions and decimals. Converting between them is necessary for accurate calculations and comparisons. For example, converting inches to centimeters often involves decimal approximations.
-
Scientific Calculations: Scientific calculations frequently involve working with both fractions and decimals. Converting between these forms allows for easier manipulation and interpretation of data.
-
Data Analysis and Statistics: In data analysis, understanding and manipulating fractional data often requires converting to decimals for easier computation and visualization.
Expanding on the Concept: Converting Other Mixed Numbers
The method used for converting 3 1/2 can be generalized to convert any mixed number to its decimal equivalent. Let's consider a few examples:
-
4 3/4: The fraction 3/4 is equivalent to 0.75 (3 divided by 4). Therefore, 4 3/4 is 4 + 0.75 = 4.75.
-
2 1/5: The fraction 1/5 is equivalent to 0.2 (1 divided by 5). Therefore, 2 1/5 is 2 + 0.2 = 2.2.
-
1 7/8: The fraction 7/8 is equivalent to 0.875 (7 divided by 8). Therefore, 1 7/8 is 1 + 0.875 = 1.875.
These examples demonstrate the consistent application of the conversion process across different mixed numbers. The key is to always convert the fractional part into its decimal equivalent before adding it to the whole number part.
Understanding Recurring Decimals
While many fractions convert to terminating decimals (like those in the examples above), some fractions yield recurring decimals, also known as repeating decimals. A recurring decimal is a decimal that has a sequence of digits that repeat infinitely. For example, 1/3 converts to 0.3333..., where the 3 repeats infinitely. This is often denoted as 0.3̅.
Dealing with recurring decimals requires understanding their representation and employing appropriate rounding techniques depending on the context of the calculation.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a fraction and a decimal?
A1: A fraction represents a part of a whole using a numerator and denominator, while a decimal represents a part of a whole using a base-10 system with a decimal point. Both represent the same underlying concept but use different notations.
Q2: How do I convert a fraction to a decimal if the denominator isn't easily converted to a power of 10?
A2: You can always perform long division: divide the numerator by the denominator. This will give you the decimal equivalent, whether it is terminating or recurring.
Q3: Are there any online tools to help with fraction-to-decimal conversions?
A3: While this article encourages understanding the process, many online calculators and converters are available to perform these conversions quickly.
Q4: Why is it important to learn how to convert fractions to decimals?
A4: This skill is crucial for various applications, including financial calculations, measurement conversions, scientific computations, and data analysis. It allows for smoother integration between different mathematical systems and facilitates efficient problem-solving.
Conclusion
Converting 3 1/2 to its decimal equivalent, 3.5, is a simple yet crucial step in understanding the relationship between fractions and decimals. This skill transcends simple arithmetic, forming the basis for more advanced mathematical concepts and practical applications across various fields. By understanding the underlying principles and mastering the different conversion methods, you'll gain a deeper appreciation for the interconnectedness of mathematical systems and enhance your problem-solving capabilities significantly. This understanding will serve as a solid foundation for tackling more complex mathematical challenges in the future. Remember to practice regularly to reinforce your understanding and build confidence in your abilities. The more you practice, the more intuitive these conversions will become.
Latest Posts
Latest Posts
-
Convert Grams To Ounces Gold
Sep 23, 2025
-
10kw Is How Many Amps
Sep 23, 2025
-
Meaning Of This Symbol
Sep 23, 2025
-
How Big Is Five Meters
Sep 23, 2025
-
1 79m To Feet And Inches
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 1/2 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.