3 1/2 As A Decimal
defexpoindia
Sep 24, 2025 · 6 min read
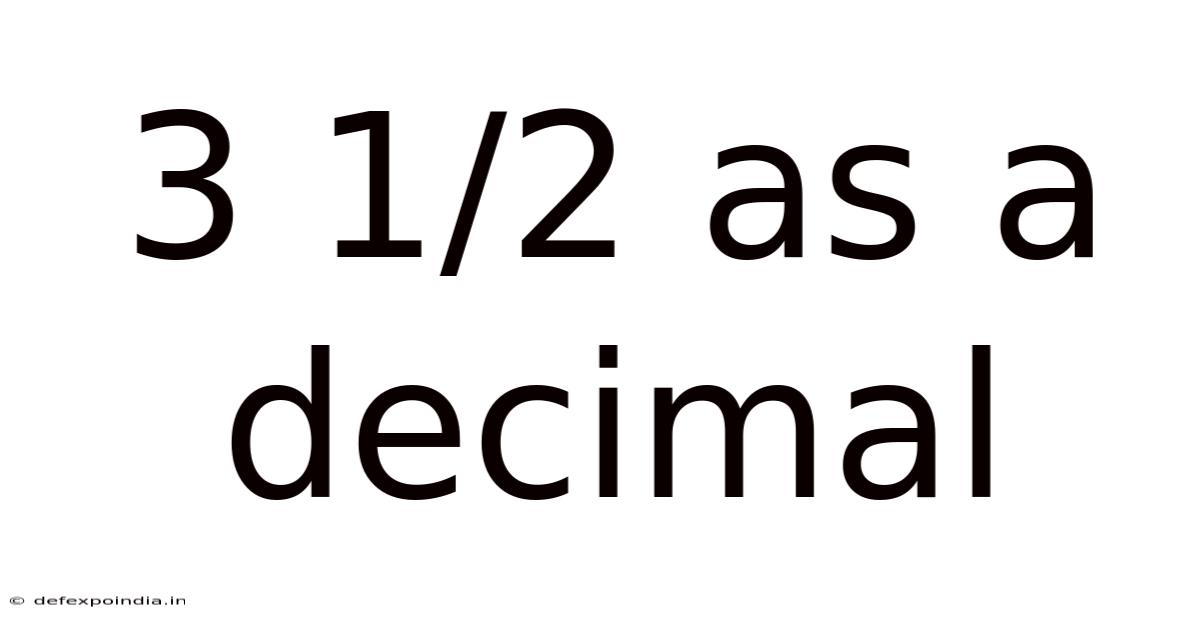
Table of Contents
Understanding 3 1/2 as a Decimal: A Comprehensive Guide
Many of us encounter fractions in our daily lives, whether it's splitting a pizza, measuring ingredients for a recipe, or solving mathematical problems. Understanding how to convert fractions to decimals is a crucial skill with applications across various fields. This article will delve deep into converting the mixed number 3 1/2 into its decimal equivalent, exploring the process step-by-step and providing a solid foundation for understanding decimal representation of fractions. We'll cover different methods, address common questions, and expand upon the broader concepts involved in fractional and decimal conversions.
Understanding Fractions and Decimals
Before diving into the conversion of 3 1/2, let's briefly review the fundamentals of fractions and decimals. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into.
A decimal, on the other hand, is a way of representing a number using base-10, where each digit to the right of the decimal point represents a power of ten. For example, 0.1 represents one-tenth (1/10), 0.01 represents one-hundredth (1/100), and so on.
Converting 3 1/2 to a Decimal: Method 1 - Direct Conversion
The simplest way to convert 3 1/2 to a decimal is to first understand what the fraction 1/2 represents. We know that 1/2 is equivalent to 0.5. This is a common and easily memorized fraction-to-decimal conversion.
Therefore, 3 1/2 can be written as 3 + 1/2 = 3 + 0.5 = 3.5.
This direct conversion method is the quickest and most intuitive for simple mixed numbers like 3 1/2. However, this method might not be as straightforward for more complex fractions.
Converting 3 1/2 to a Decimal: Method 2 - Dividing the Numerator by the Denominator
This method is more versatile and can be applied to any fraction, regardless of its complexity. To use this method, we first need to convert the mixed number 3 1/2 into an improper fraction.
An improper fraction has a numerator larger than or equal to its denominator. To convert 3 1/2 into an improper fraction, we multiply the whole number (3) by the denominator (2) and then add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
3 x 2 + 1 = 7
So, 3 1/2 becomes 7/2.
Now, we divide the numerator (7) by the denominator (2):
7 ÷ 2 = 3.5
Therefore, 3 1/2 is equal to 3.5. This method reinforces the understanding that a fraction essentially represents a division problem.
Converting 3 1/2 to a Decimal: Method 3 - Using Percentage
Another approach involves converting the fraction to a percentage and then converting the percentage to a decimal. We know that 1/2 is equivalent to 50%.
Therefore, 3 1/2 represents 3 + 50% = 350%.
To convert a percentage to a decimal, we divide the percentage by 100:
350% ÷ 100 = 3.5
This method provides an alternative perspective and further strengthens the connection between fractions, percentages, and decimals.
Expanding on Decimal Representation: Place Value
Understanding place value is crucial for grasping the significance of decimals. In the decimal representation of 3.5, the digit '3' represents 3 ones, while the digit '5' represents 5 tenths (5/10). Each position to the right of the decimal point represents a decreasing power of 10: tenths, hundredths, thousandths, and so on. This system is based on the base-10 number system, making it intuitive and easy to work with.
Applications of Decimal Representation
The decimal representation of 3 1/2, or 3.5, finds numerous applications in everyday life and various fields:
- Measurements: Lengths, weights, and volumes are often expressed using decimals. For example, 3.5 meters or 3.5 kilograms.
- Finance: Monetary values are typically expressed using decimals. For instance, $3.50.
- Data analysis: Decimals are essential for representing and analyzing data, particularly in scientific and statistical applications.
- Computer science: Decimals are fundamental in computer programming and digital representation of numbers.
Working with More Complex Fractions
The methods discussed above can be extended to convert more complex fractions into decimals. Let's consider the example of 7/8.
Following Method 2 (dividing the numerator by the denominator):
7 ÷ 8 = 0.875
Therefore, 7/8 is equal to 0.875.
For fractions with repeating decimals (like 1/3 = 0.333...), you might need to round the decimal to a certain number of decimal places based on the required level of precision.
Frequently Asked Questions (FAQ)
Q1: Why is it important to know how to convert fractions to decimals?
A1: Converting fractions to decimals is a fundamental mathematical skill essential for various applications, from everyday calculations to complex scientific and engineering problems. It allows for easier comparison and manipulation of numbers in many contexts.
Q2: Can all fractions be expressed as terminating decimals?
A2: No. Fractions with denominators that have prime factors other than 2 and 5 (when expressed in their simplest form) will result in repeating decimals. For example, 1/3, 1/7, and 1/11 result in repeating decimals.
Q3: What is the difference between a mixed number and an improper fraction?
A3: A mixed number consists of a whole number and a fraction (like 3 1/2). An improper fraction has a numerator larger than or equal to its denominator (like 7/2). Both represent the same quantity but are expressed differently.
Q4: How can I improve my skills in converting fractions to decimals?
A4: Practice is key. Start with simple fractions and gradually increase the complexity. Understanding the underlying principles of fractions, decimals, and the division process will make the conversion more intuitive. You can also use online calculators and educational resources to reinforce your learning and check your answers.
Conclusion
Converting 3 1/2 to a decimal, resulting in 3.5, is a straightforward process that can be achieved through several methods. Understanding these methods, along with the broader concepts of fractions and decimals, is crucial for developing a solid mathematical foundation. This understanding empowers you to tackle more complex fractional and decimal conversions confidently and effectively, paving the way for success in various mathematical and real-world applications. The ability to seamlessly transition between these two numerical representations is a skill that enhances problem-solving capabilities and deepens your comprehension of fundamental mathematical principles. Continue practicing and exploring these concepts to build a strong understanding of this essential mathematical skill.
Latest Posts
Latest Posts
-
How Many Inches In 80cm
Sep 24, 2025
-
300cm To Inches And Feet
Sep 24, 2025
-
30 Inch Waist In Cm
Sep 24, 2025
-
How Much Is 152 Kg
Sep 24, 2025
-
How Big Is 20 M
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 3 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.