2 1/3 In Decimal Form
defexpoindia
Sep 20, 2025 · 5 min read
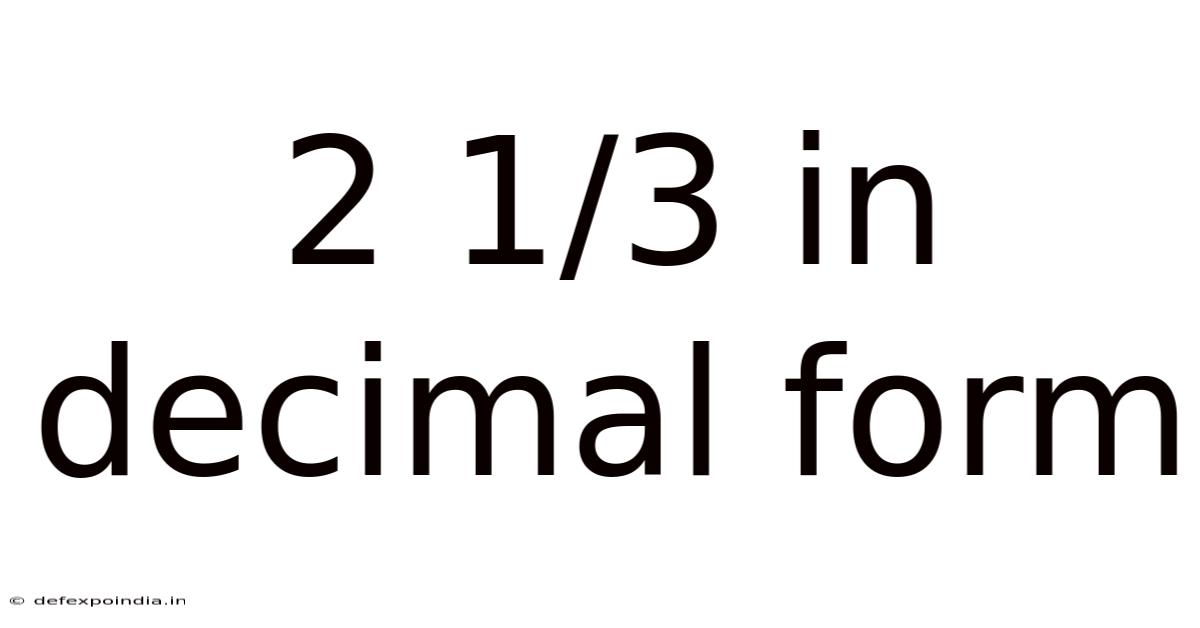
Table of Contents
Unveiling the Decimal Mystery: Understanding 2 1/3 in Decimal Form
Converting fractions to decimals might seem daunting at first, but it's a fundamental skill with widespread applications in math, science, and everyday life. This comprehensive guide will walk you through the process of converting the mixed number 2 1/3 into its decimal equivalent, exploring different methods and delving into the underlying mathematical principles. We'll cover various approaches, address common questions, and ensure you gain a solid understanding of this essential concept. By the end, you'll not only know the decimal value of 2 1/3 but also possess the tools to tackle similar conversions confidently.
Understanding Mixed Numbers and Fractions
Before we dive into the conversion, let's briefly review the terminology. A mixed number combines a whole number and a fraction, like 2 1/3. This represents two whole units plus one-third of another unit. The fraction 1/3 indicates one part out of three equal parts of a whole. Converting this to a decimal means expressing it as a number using the base-10 system, with a decimal point separating the whole number part from the fractional part.
Method 1: Converting the Fraction to a Decimal Directly
The most straightforward approach involves converting the fraction 1/3 into a decimal first and then adding the whole number part. To do this, we perform the division:
1 ÷ 3 = 0.3333...
Notice the repeating decimal. The number 3 repeats infinitely. This is represented mathematically as 0.3̅, with a bar above the 3 to denote the repeating digit. Now, add the whole number part:
2 + 0.3̅ = 2.3̅
Therefore, 2 1/3 in decimal form is 2.3̅ or approximately 2.333. While we use an approximation for practical purposes, it's crucial to remember the true decimal value is a repeating decimal.
Method 2: Converting the Mixed Number to an Improper Fraction
An alternative method involves first converting the mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator. To do this:
- Multiply the whole number by the denominator: 2 * 3 = 6
- Add the numerator: 6 + 1 = 7
- Keep the same denominator: 7/3
Now, we have the improper fraction 7/3. To convert this to a decimal, we perform the division:
7 ÷ 3 = 2.3333... = 2.3̅
This confirms our previous result: 2 1/3 is equal to 2.3̅ in decimal form.
Method 3: Using Long Division
Long division provides a visual and methodical approach to converting fractions to decimals. Let's use this method for 7/3:
2.333...
3 | 7.000
6
---
10
9
---
10
9
---
10
9
---
1
As you can see, the remainder 1 keeps repeating, resulting in the repeating decimal 2.3̅. This reinforces the accuracy of our previous calculations.
Understanding Repeating Decimals
The decimal representation of 2 1/3 highlights an important concept: repeating decimals. These decimals have a sequence of digits that repeats infinitely. Understanding repeating decimals is essential for working with fractions that have denominators that are not factors of 10 (i.e., 10, 100, 1000, etc.). Not all fractions result in repeating decimals. For example, 1/4 = 0.25, which is a terminating decimal. Terminating decimals have a finite number of digits after the decimal point.
Practical Applications of Decimal Conversions
Converting fractions to decimals is a critical skill with numerous real-world applications:
-
Measurements: Many measuring tools display measurements in decimal form. Converting fractional measurements to decimals ensures accuracy and ease of calculation. Imagine calculating the area of a room with dimensions involving fractions – converting to decimals streamlines the process.
-
Financial Calculations: Dealing with money often requires decimal calculations. Understanding the decimal equivalent of fractions is vital for accurate financial computations, particularly when calculating percentages, interest rates, or discounts.
-
Scientific Calculations: Science and engineering frequently utilize decimals in various formulas and calculations. Converting fractions to decimals allows for easier manipulation of data and consistent calculations.
-
Data Analysis: Data analysis often involves working with datasets containing both fractional and decimal values. Converting between these forms ensures data consistency and facilitates efficient analysis using statistical tools.
-
Everyday Problem Solving: Many everyday situations require converting between fractions and decimals. For instance, sharing items, calculating baking recipes, or even understanding sale prices all benefit from understanding this conversion.
Frequently Asked Questions (FAQ)
Q: Why does 1/3 result in a repeating decimal?
A: The reason 1/3 produces a repeating decimal is because its denominator, 3, is not a factor of any power of 10. To express a fraction as a decimal, we essentially divide the numerator by the denominator. When the denominator doesn't divide evenly into powers of 10, the division process continues indefinitely, leading to a repeating decimal.
Q: How can I round a repeating decimal?
A: Rounding a repeating decimal depends on the desired level of precision. For example, you might round 2.3̅ to 2.33 if two decimal places are sufficient, or to 2.333 if three decimal places are required. The more decimal places you include, the more accurate the approximation will be.
Q: Are there other fractions that result in repeating decimals?
A: Yes, many fractions result in repeating decimals. In general, any fraction whose denominator contains prime factors other than 2 and 5 will result in a repeating decimal.
Q: How do I convert a repeating decimal back to a fraction?
A: Converting a repeating decimal back to a fraction involves a process of algebraic manipulation. Let's illustrate this with 0.3̅:
- Let x = 0.3̅
- Multiply both sides by 10: 10x = 3.3̅
- Subtract the first equation from the second: 10x - x = 3.3̅ - 0.3̅
- This simplifies to 9x = 3
- Solve for x: x = 3/9 = 1/3
This shows that the repeating decimal 0.3̅ is equivalent to the fraction 1/3.
Conclusion: Mastering Decimal Conversions
Converting fractions to decimals is a fundamental mathematical skill with far-reaching applications. Understanding the different methods – direct conversion, improper fraction conversion, and long division – empowers you to confidently tackle various conversion problems. While the concept of repeating decimals might seem complex at first, grasping its meaning is crucial for a thorough understanding of decimal representation. By practicing these methods and addressing common questions, you'll build a strong foundation for tackling more complex mathematical and real-world problems that involve fractions and decimals. Remember, the key is practice and understanding the underlying mathematical principles. With enough practice, converting fractions like 2 1/3 to its decimal equivalent, 2.3̅, will become second nature.
Latest Posts
Latest Posts
-
How Far Is 300 Yd
Sep 21, 2025
-
Whats 200 Cm In Feet
Sep 21, 2025
-
What Is 100f In C
Sep 21, 2025
-
50 Cm Cuantas Pulgadas Son
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2 1/3 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.