12 Times 12 Times 12
defexpoindia
Sep 13, 2025 · 6 min read
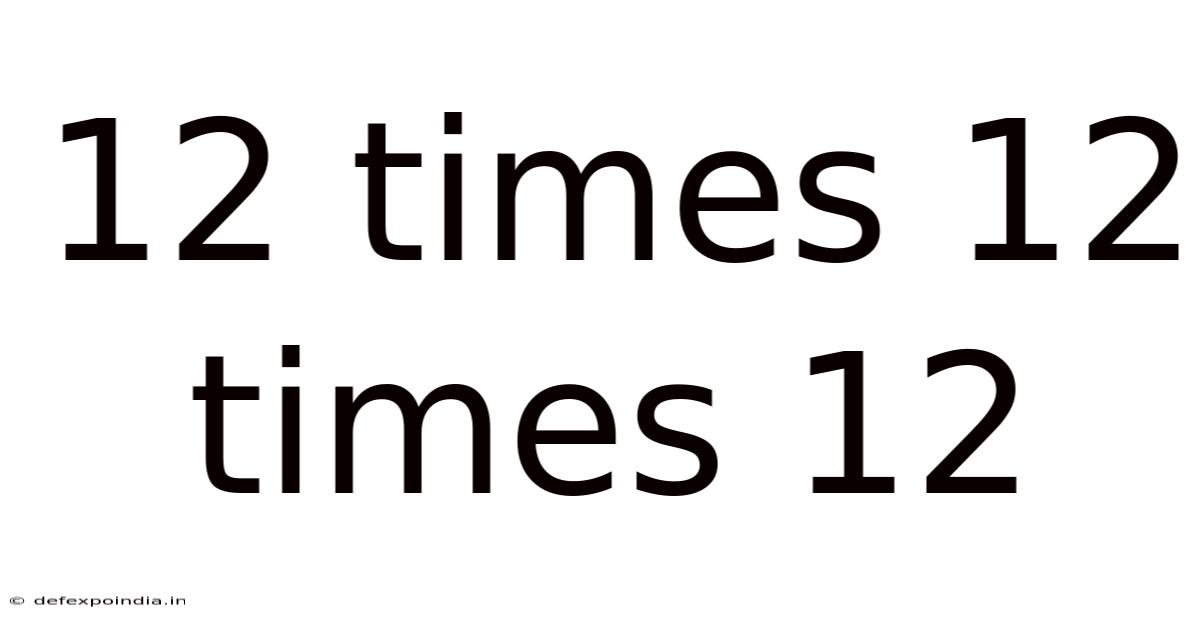
Table of Contents
Decoding 12 x 12 x 12: A Deep Dive into Cubic Calculations and Their Applications
Have you ever wondered what the result of 12 multiplied by 12, then multiplied by 12 again truly represents? Beyond a simple numerical calculation, understanding 12 x 12 x 12 opens doors to exploring concepts in mathematics, geometry, and even real-world applications. This article will delve into the calculation itself, explore its geometric interpretation, examine its relevance in various fields, and answer frequently asked questions. Let's embark on this numerical journey together!
Understanding the Calculation: 12 x 12 x 12 = ?
The calculation 12 x 12 x 12 is a straightforward example of cubing a number. Cubing means raising a number to the power of three (represented as x³). In simpler terms, it's multiplying a number by itself three times. Let's break it down:
- 12 x 12 = 144: This is the first step, a familiar multiplication fact.
- 144 x 12 = 1728: This is the final result of cubing 12.
Therefore, 12 x 12 x 12 = 1728. This seemingly simple calculation has far-reaching implications when we consider its geometric representation and real-world applications.
The Geometric Interpretation: Volume and Cubes
The number 1728 has a significant geometric meaning. It represents the volume of a cube whose sides each measure 12 units. Imagine a perfectly formed cube, like a Rubik's Cube, with each edge measuring 12 centimeters, 12 inches, or 12 any other unit of length. The volume—the amount of space enclosed within the cube—is calculated by multiplying the length, width, and height together. Since all sides of a cube are equal, this translates to 12 x 12 x 12 = 1728 cubic units.
This visualization helps solidify the understanding of cubing a number. It's not just an abstract mathematical operation; it has a tangible, three-dimensional representation. This connection between numerical calculations and real-world geometry is crucial for developing a strong foundation in mathematics.
Applications of 12 x 12 x 12 in Various Fields
The number 1728, derived from 12 x 12 x 12, appears in various unexpected places across different fields:
-
Construction and Engineering: Understanding cubic volume is fundamental in construction. Calculations involving cubic feet or cubic meters are used to determine the volume of materials needed for projects, such as concrete foundations or the amount of earth to be excavated. The number 1728 might directly relate to the volume of specific building elements or materials.
-
Packaging and Shipping: Companies involved in shipping and packaging need to calculate the volume of boxes to optimize space and shipping costs. If a box has dimensions of 12 x 12 x 12 inches, its volume will be 1728 cubic inches, a crucial piece of information for logistical planning.
-
Data Storage: In computer science, data storage is often measured in bytes, kilobytes, megabytes, and so on. Understanding cubic calculations can be helpful in visualizing the scale of large data sets. While not a direct application of 1728 specifically, the underlying concept of cubic growth in data storage is relevant.
-
Fluid Dynamics: In physics and engineering, fluid dynamics involves calculating the volume of liquids or gases. Knowing the volume of a container, possibly measured in cubic units, is crucial in understanding fluid behavior and properties.
-
Finance and Investment: Compound interest calculations involve exponential growth, which is conceptually related to cubic calculations. While not directly utilizing 1728, the principles of exponentiation and growth are crucial to both.
Expanding the Concept: Cubes and Beyond
While we focused on 12 x 12 x 12, the concept of cubing numbers extends far beyond this specific example. It’s a fundamental operation in algebra and has significant implications in various branches of mathematics:
-
Algebraic Expressions: Cubing is a key operation in simplifying and solving algebraic expressions. Understanding how to manipulate cubed variables is essential for advanced algebraic manipulations.
-
Calculus: Derivatives and integrals often involve functions that include cubed terms. Mastering the concepts related to cubing numbers is a foundational step towards understanding more complex mathematical concepts in calculus.
-
Geometry and 3D Shapes: Cubing is integral to calculating the volume of various three-dimensional shapes. This extends beyond cubes to include rectangular prisms, pyramids, and other three-dimensional geometric forms.
Further Exploration: Number Theory and Factorization
The number 1728 itself offers further mathematical exploration. We can analyze its factors and delve into its properties within number theory:
-
Prime Factorization: Breaking down 1728 into its prime factors reveals its fundamental building blocks. 1728 can be factored as 2⁶ x 3³. This provides further insight into the number's mathematical structure.
-
Divisibility: Understanding the prime factorization helps determine which numbers divide 1728 evenly. This has implications in various mathematical applications, such as solving equations and working with fractions.
-
Number Patterns: The number 1728 is involved in various mathematical patterns and sequences. Exploring these patterns can enhance your understanding of number theory and mathematical relationships.
Frequently Asked Questions (FAQ)
-
Q: What is the cube root of 1728?
- A: The cube root of 1728 is 12, because 12 x 12 x 12 = 1728. The cube root is the number that, when multiplied by itself three times, equals the original number.
-
Q: Are there any real-world objects that have a volume of exactly 1728 cubic units?
- A: While not common for everyday objects, many manufactured items could potentially have a volume of approximately 1728 cubic units. This could include specific containers, storage units, or custom-made objects. The exact dimensions would depend on the unit of measurement used (cubic centimeters, cubic inches, cubic feet, etc.).
-
Q: How can I calculate the volume of other shapes besides cubes?
- A: The formula for calculating volume varies depending on the shape. For a rectangular prism (a box), it's length x width x height. For a sphere, it's (4/3)πr³. For other shapes, specific formulas must be applied based on their geometric properties. Consulting geometry resources will provide the relevant formulas.
-
Q: Is there a relationship between cubing numbers and other mathematical concepts?
- A: Yes, cubing is deeply intertwined with other mathematical concepts. It’s directly related to exponents, powers, roots, volume calculations, and more complex topics like calculus and algebra. Understanding cubing is a foundational step in exploring many advanced mathematical areas.
Conclusion: Beyond the Calculation
The seemingly simple calculation of 12 x 12 x 12 = 1728 provides a gateway to understanding fundamental mathematical principles and their real-world applications. From visualizing cubic volume to exploring its relevance in construction, packaging, and various scientific fields, this seemingly simple calculation reveals a depth of mathematical significance. By exploring the geometric interpretations, practical applications, and related mathematical concepts, we can appreciate the rich tapestry of mathematical knowledge woven into this single calculation. This journey highlights the interconnectedness of different mathematical areas and encourages further exploration of the fascinating world of numbers. So, the next time you encounter a cubic calculation, remember the multifaceted nature of this seemingly simple mathematical operation and its profound implications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 12 Times 12 Times 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.