12 1/5 As A Decimal
defexpoindia
Sep 22, 2025 · 5 min read
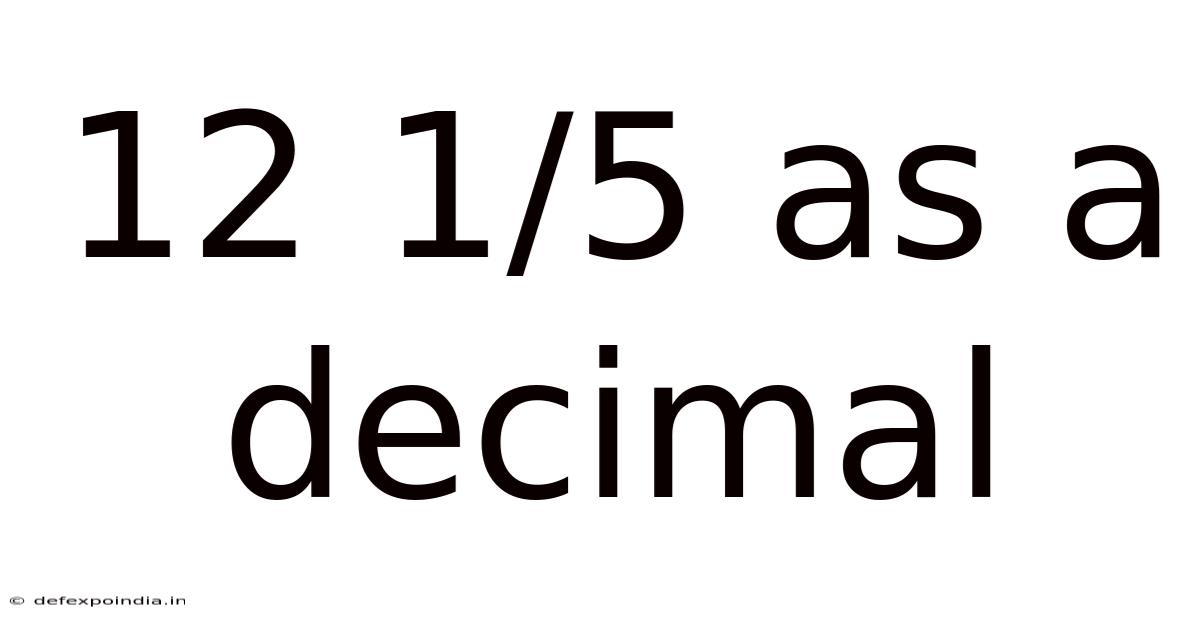
Table of Contents
12 1/5 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will explore the conversion of the mixed number 12 1/5 into its decimal equivalent, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also address common misconceptions and answer frequently asked questions, ensuring a thorough understanding of this important concept. Understanding this seemingly simple conversion provides a solid foundation for more complex decimal and fraction manipulations.
Understanding Mixed Numbers and Decimals
Before diving into the conversion process, let's briefly review the definitions of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 12 1/5. This represents 12 whole units plus one-fifth of another unit. A decimal, on the other hand, represents a number using a base-ten system, where digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, etc.).
Converting 12 1/5 to a Decimal: Step-by-Step
The conversion of 12 1/5 to a decimal involves two key steps:
Step 1: Convert the Fraction to a Decimal
The fraction 1/5 represents one part out of five equal parts. To convert it to a decimal, we perform the division: 1 ÷ 5.
1 ÷ 5 = 0.2
Therefore, 1/5 is equivalent to 0.2.
Step 2: Combine the Whole Number and the Decimal
Now, we combine the whole number part (12) with the decimal equivalent of the fraction (0.2):
12 + 0.2 = 12.2
Therefore, 12 1/5 as a decimal is 12.2.
Alternative Methods for Conversion
While the above method is the most straightforward, let's explore a couple of alternative approaches:
Method 1: Converting to an Improper Fraction First
We can convert the mixed number 12 1/5 into an improper fraction before converting to a decimal. An improper fraction has a numerator larger than or equal to its denominator.
To convert 12 1/5 to an improper fraction:
- Multiply the whole number by the denominator: 12 * 5 = 60
- Add the numerator: 60 + 1 = 61
- Keep the same denominator: The improper fraction is 61/5.
Now, divide the numerator by the denominator:
61 ÷ 5 = 12.2
This confirms our previous result. This method is particularly useful when dealing with more complex mixed numbers.
Method 2: Using Decimal Equivalents of Common Fractions
Memorizing the decimal equivalents of common fractions can expedite the conversion process. For example, knowing that 1/5 = 0.2 allows for a quick conversion without performing long division. Similarly, knowing that 1/2 = 0.5, 1/4 = 0.25, and 1/10 = 0.1 can significantly speed up calculations involving these fractions. This method relies on prior knowledge and memorization but can be very efficient for familiar fractions.
Understanding the Mathematical Principles
The conversion of fractions to decimals fundamentally involves division. The fraction a/b represents the division a ÷ b. When performing this division, the result can be a terminating decimal (like 0.2 in our example) or a repeating decimal (e.g., 1/3 = 0.333...). A terminating decimal has a finite number of digits after the decimal point, while a repeating decimal has a pattern of digits that repeats infinitely. The nature of the denominator (b) determines whether the decimal will be terminating or repeating. If the denominator can be expressed solely as a product of 2s and 5s (powers of 10), the resulting decimal will terminate. Otherwise, it will be a repeating decimal. In the case of 1/5, the denominator is 5, a power of 5, resulting in a terminating decimal.
Applications of Decimal Conversions
The ability to convert fractions to decimals is essential in various mathematical and real-world contexts:
- Financial calculations: Working with percentages, interest rates, and monetary amounts frequently requires converting fractions to decimals.
- Measurement and engineering: Many measurement systems utilize decimal notation. Converting fractional measurements to decimals is crucial for precision and accuracy.
- Scientific computations: Scientific calculations often involve decimal numbers, making the conversion of fractions necessary for consistency.
- Data analysis and statistics: Representing data in decimal form is often more convenient for analysis and interpretation.
- Computer programming: Many programming languages handle decimal numbers more efficiently than fractions.
Common Misconceptions
A common misconception is believing that all fractions convert to terminating decimals. As discussed earlier, fractions with denominators that are not solely products of 2s and 5s result in repeating decimals. Another misconception is incorrectly performing the division when converting a fraction to a decimal. Care must be taken to correctly divide the numerator by the denominator.
Frequently Asked Questions (FAQ)
Q: Can all fractions be expressed as decimals?
A: Yes, all fractions can be expressed as decimals. The resulting decimal may be either terminating or repeating.
Q: How do I convert a repeating decimal back to a fraction?
A: Converting a repeating decimal to a fraction requires a specific algebraic process. This involves setting the decimal equal to a variable, multiplying by a power of 10 to shift the repeating part, subtracting the original equation, and solving for the variable.
Q: What if I have a mixed number with a fraction that doesn't have a simple decimal equivalent, like 12 1/7?
A: You would follow the same process: convert the fraction 1/7 to a decimal through division (1 ÷ 7 = 0.142857...), and then add the whole number (12). This will result in a repeating decimal.
Q: Are there any online calculators or tools that can help with these conversions?
A: Yes, many online calculators are available that can quickly convert fractions to decimals and vice versa. However, understanding the underlying mathematical principles is crucial for developing a strong foundation in mathematics.
Conclusion
Converting 12 1/5 to a decimal, resulting in 12.2, is a straightforward process that highlights the fundamental relationship between fractions and decimals. This conversion, and the broader understanding of fraction-to-decimal conversion, is a critical skill across numerous academic and practical applications. Mastering this skill provides a strong foundation for tackling more complex mathematical problems and enhances problem-solving abilities in various fields. By understanding the step-by-step process, alternative methods, and the underlying mathematical principles, you can confidently tackle similar conversions and further develop your mathematical fluency. Remember, consistent practice and a focus on understanding the "why" behind the procedures are key to mastering this important concept.
Latest Posts
Latest Posts
-
400 Meters Converted To Feet
Sep 22, 2025
-
7k Is How Many Miles
Sep 22, 2025
-
18 20 As A Decimal
Sep 22, 2025
-
How Long Is 20 Feet
Sep 22, 2025
-
How Big Is 3 Feet
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 12 1/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.