11 20 As A Percent
defexpoindia
Sep 20, 2025 · 5 min read
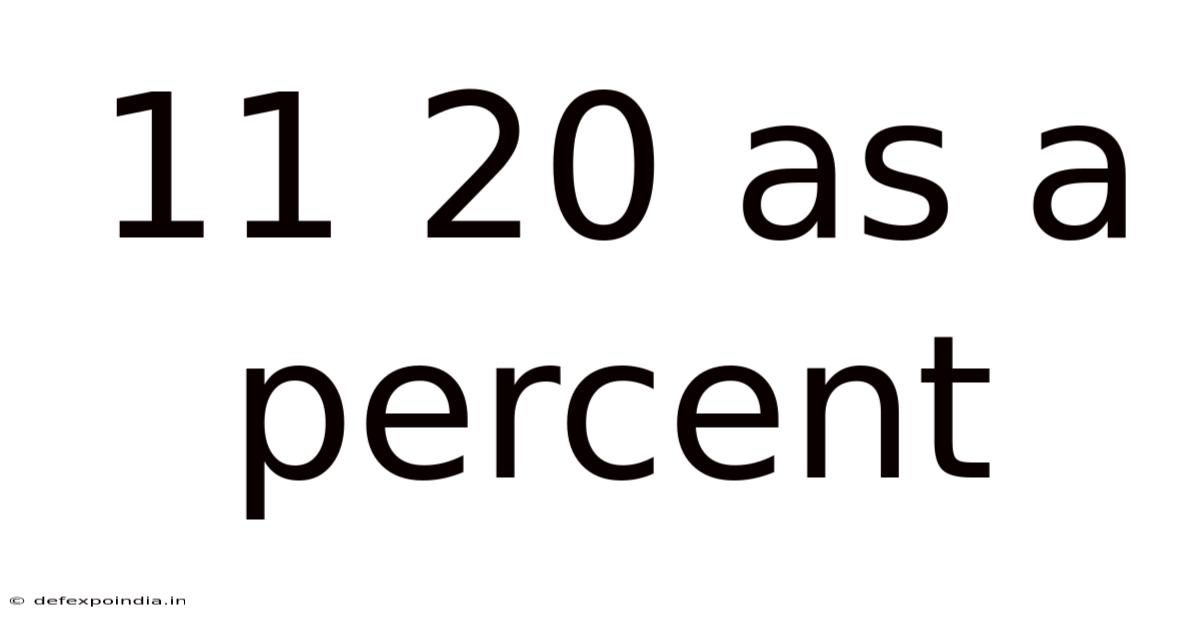
Table of Contents
11/20 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding statistics and data analysis. This article provides a comprehensive guide on how to convert the fraction 11/20 into a percentage, explaining the underlying principles and offering practical examples. We'll explore different methods, address common misconceptions, and delve into the significance of understanding fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before we dive into the conversion process, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 11/20, 11 is the numerator and 20 is the denominator. This means we are considering 11 parts out of a total of 20 parts.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" is used to represent "percent," which literally means "out of 100". Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Direct Conversion Using Division
The most straightforward method to convert a fraction to a percentage is through division. We follow these steps:
-
Divide the numerator by the denominator: In our case, we divide 11 by 20. This gives us 0.55.
-
Multiply the result by 100: To express the decimal as a percentage, we multiply the decimal result (0.55) by 100. This yields 55.
-
Add the percentage symbol: Finally, we add the "%" symbol to indicate that the result is a percentage.
Therefore, 11/20 as a percent is 55%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction with a denominator of 100. This method relies on the understanding that percentages are fractions out of 100.
-
Determine the scaling factor: We need to find a number that, when multiplied by the original denominator (20), results in 100. In this case, 20 multiplied by 5 equals 100.
-
Multiply both the numerator and the denominator by the scaling factor: We multiply both the numerator (11) and the denominator (20) by 5. This gives us the equivalent fraction 55/100.
-
Express as a percentage: Since 55/100 means 55 out of 100, this is equivalent to 55%.
Method 3: Using Proportions
Proportions offer a more formal approach to solve this type of problem. We set up a proportion to find the equivalent percentage:
11/20 = x/100
To solve for 'x', we cross-multiply:
20x = 1100
Then, we divide both sides by 20:
x = 1100/20 = 55
Therefore, x = 55, meaning 11/20 is equivalent to 55%.
Illustrative Examples: Real-World Applications
Understanding fraction-to-percentage conversion is crucial in numerous real-world scenarios. Let's consider a few examples:
-
Sales and Discounts: A store offers a 11/20 discount on a product. To determine the percentage discount, we convert 11/20 to a percentage, which is 55%. This means the customer receives a 55% discount.
-
Test Scores: If a student answers 11 out of 20 questions correctly on a test, their score is 11/20. Converting this fraction to a percentage gives us 55%, representing their performance on the test.
-
Data Analysis: In statistical analysis, fractions are often used to represent proportions. Converting these fractions to percentages allows for easier interpretation and comparison of data. For instance, if 11 out of 20 respondents prefer a particular product, this translates to a 55% preference rate.
Common Mistakes to Avoid
While the conversion process is relatively simple, some common mistakes can lead to inaccurate results:
-
Incorrect order of operations: Remember to divide the numerator by the denominator before multiplying by 100. Reversing this order will lead to an incorrect answer.
-
Forgetting the percentage symbol: Always include the "%" symbol to denote the final answer as a percentage. Omitting this symbol is a common oversight.
-
Rounding errors: Depending on the context, rounding the decimal result to a certain number of decimal places might be necessary. However, ensure that rounding does not significantly affect the accuracy of the final percentage.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, any fraction can be converted to a percentage using the methods described above. However, some fractions may result in repeating decimals when converted to percentages.
Q2: What if the fraction is an improper fraction (numerator > denominator)?
A2: The process remains the same. Divide the numerator by the denominator, multiply by 100, and add the "%" symbol. The resulting percentage will be greater than 100%.
Q3: Is there a quick way to convert simple fractions to percentages?
A3: Yes, for common fractions like 1/2, 1/4, 1/5, etc., memorizing their percentage equivalents can speed up calculations. For example, 1/2 = 50%, 1/4 = 25%, 1/5 = 20%.
Q4: What are the practical applications of understanding fraction-to-percentage conversion beyond basic math?
A4: This skill is essential in numerous fields, including finance (calculating interest rates, discounts, and profit margins), statistics (analyzing data and presenting findings), and everyday situations (calculating tips, sales tax, and proportions).
Conclusion
Converting fractions to percentages is a valuable skill applicable across various domains. Understanding the different methods – direct division, equivalent fractions, and proportions – allows for flexibility in choosing the most efficient approach. Mastering this conversion enhances mathematical fluency and problem-solving skills, contributing to a more comprehensive understanding of numerical relationships and their real-world applications. By avoiding common mistakes and practicing regularly, you can confidently navigate fraction-to-percentage conversions in various contexts. Remember that the core principle remains consistent: a percentage represents a fraction out of 100.
Latest Posts
Latest Posts
-
Set Timer For 60 Minutes
Sep 20, 2025
-
How Long Is 500 Ft
Sep 20, 2025
-
What Is 20x30cm In Inches
Sep 20, 2025
-
800 Grams Converted To Pounds
Sep 20, 2025
-
90 Deg Celsius To Fahrenheit
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 11 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.