1 9/100 As A Percent
defexpoindia
Sep 22, 2025 · 5 min read
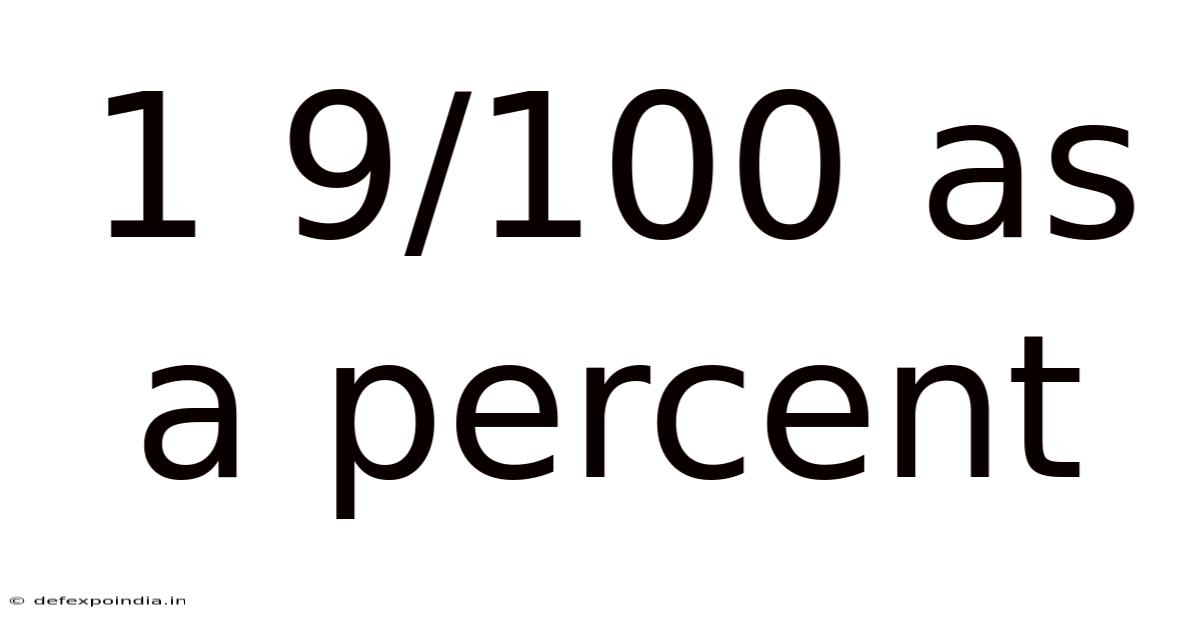
Table of Contents
1/9/100 as a Percent: Understanding Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics. This article will comprehensively explore how to convert the fraction 1/9/100 into a percentage, delving into the underlying concepts and providing a step-by-step guide. We'll also address common misconceptions and answer frequently asked questions, ensuring a complete understanding of this essential mathematical conversion.
Introduction: The Interplay of Fractions, Decimals, and Percentages
Fractions, decimals, and percentages are different ways of representing parts of a whole. A fraction expresses a part as a ratio of two numbers (numerator and denominator). A decimal represents a part using base-10 notation. A percentage expresses a part as a fraction of 100. Mastering the conversion between these three forms is crucial for various applications, from everyday calculations to advanced mathematical problems. This article focuses specifically on converting the complex fraction 1/9/100 into its percentage equivalent. The seemingly simple notation presents a unique challenge because of the nested fraction, requiring a careful understanding of order of operations.
Understanding the Complex Fraction 1/9/100
The notation "1/9/100" is ambiguous. It's crucial to clarify the intended meaning before proceeding with the conversion. There are two possible interpretations:
-
Interpretation 1: (1/9)/100: This interpretation suggests a fraction of a fraction. We first calculate 1/9 and then divide the result by 100.
-
Interpretation 2: 1/(9/100): This interpretation indicates that 1 is divided by the fraction 9/100.
We will address both interpretations, demonstrating the conversion process for each. It's vital to emphasize the importance of clear and unambiguous notation in mathematics to avoid potential errors.
Method 1: Converting (1/9)/100 to a Percentage
This interpretation presents a nested fraction. Let's break it down step by step:
-
Calculate 1/9: Dividing 1 by 9 gives us approximately 0.1111 (the decimal representation is recurring).
-
Divide by 100: Now, we divide the result (approximately 0.1111) by 100. This equals 0.001111.
-
Convert to Percentage: To express this decimal as a percentage, we multiply by 100%. Therefore, (1/9)/100 is approximately 0.1111%.
In summary: (1/9)/100 ≈ 0.1111%
Method 2: Converting 1/(9/100) to a Percentage
This interpretation involves dividing 1 by the fraction 9/100. The process is as follows:
-
Simplify the Divisor: Recall that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 9/100 is 100/9.
-
Perform the Multiplication: We now multiply 1 by 100/9: 1 * (100/9) = 100/9
-
Convert to Decimal: Dividing 100 by 9 gives us approximately 11.1111.
-
Convert to Percentage: Multiplying the decimal by 100% yields approximately 1111.11%.
In summary: 1/(9/100) ≈ 1111.11%
Explanation of the Discrepancy
The significant difference between the results (approximately 0.1111% vs. approximately 1111.11%) highlights the critical importance of correct interpretation of mathematical notation. The seemingly minor difference in the placement of parentheses drastically alters the outcome. This exemplifies the need for precision and clarity when working with fractions and other mathematical expressions.
The Importance of Order of Operations (PEMDAS/BODMAS)
The difference in results underscores the importance of following the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Correctly interpreting and applying the order of operations is paramount to achieving accurate calculations. In our examples, the parentheses significantly altered the order of operations and therefore the final answer.
Practical Applications
Understanding fraction-to-percentage conversions is crucial in numerous real-world scenarios:
- Financial Calculations: Calculating interest rates, discounts, profit margins, and tax rates.
- Data Analysis: Representing data proportions in charts and graphs.
- Scientific Research: Expressing experimental results and statistical probabilities.
- Everyday Life: Calculating tips, sales tax, and portion sizes.
Frequently Asked Questions (FAQ)
-
Q: Why is the percentage different depending on the interpretation? A: Because the placement of parentheses changes the order of operations, resulting in different calculations and thus different final answers. This emphasizes the importance of clear and unambiguous notation.
-
Q: Can I use a calculator for these conversions? A: Yes, most scientific calculators can handle these types of calculations. However, it's essential to enter the expression correctly according to the intended interpretation.
-
Q: What if the fraction is more complex? A: The same principles apply. Always simplify the fraction first (if possible), then convert to a decimal and finally to a percentage by multiplying by 100%.
-
Q: Are there other ways to represent 1/9/100? A: Yes, depending on the interpretation, it can also be represented as a decimal (approximately 0.001111 or approximately 11.1111) or as a ratio (1:900 or 100:9, depending on the interpretation).
Conclusion: Accuracy and Clarity in Mathematical Notation
Converting 1/9/100 into a percentage requires careful attention to the notation. The two possible interpretations, (1/9)/100 and 1/(9/100), yield vastly different results due to the order of operations. This highlights the critical role of precise notation in mathematics. Understanding fractions, decimals, and percentages, along with the rules of order of operations, is fundamental to accurate calculations in numerous applications. By mastering these concepts, you can confidently navigate mathematical challenges and apply your knowledge to real-world problems. Remember to always clarify the meaning of ambiguous notation to avoid errors and ensure accuracy in your calculations. The correct application of the principles outlined in this article will provide you with the tools to handle similar conversion problems effectively.
Latest Posts
Latest Posts
-
How Long Is 22 Meters
Sep 22, 2025
-
20 Cm Equal To Inches
Sep 22, 2025
-
90 Degrees Farenheit To Celcius
Sep 22, 2025
-
700 Square Feet In Meters
Sep 22, 2025
-
How Much Is 20 Oz
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 9/100 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.