1 7/8 As A Decimal
defexpoindia
Sep 14, 2025 · 5 min read
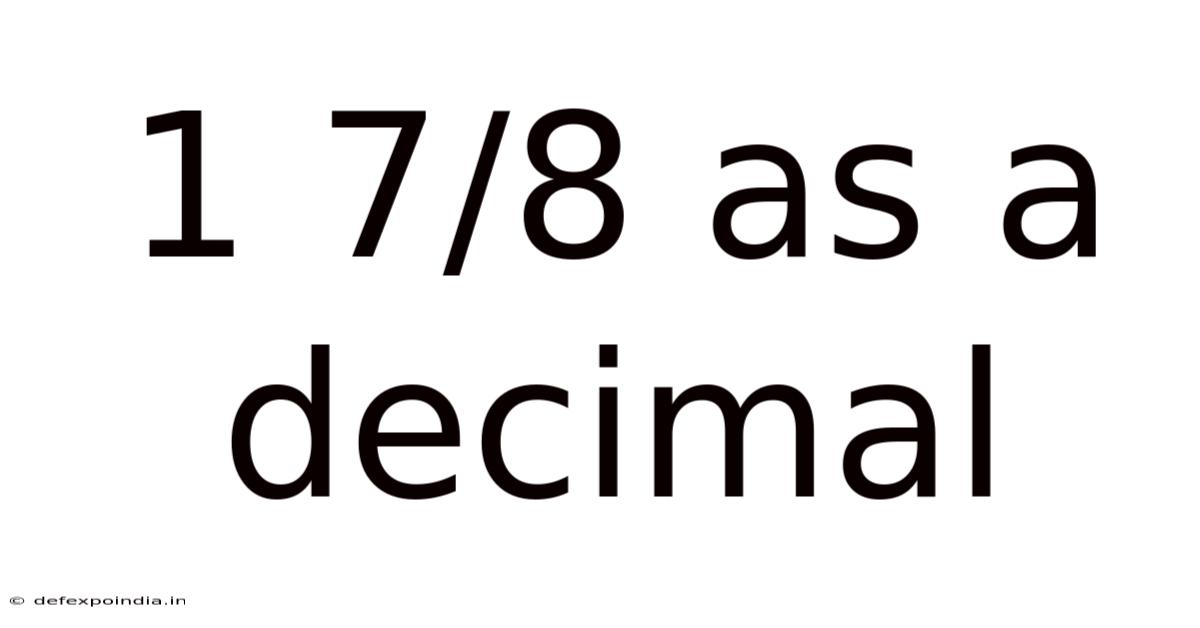
Table of Contents
1 7/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the mixed number 1 7/8 into its decimal equivalent, exploring different methods and providing a deeper understanding of the underlying principles. We'll also address common questions and misconceptions, ensuring you're confident in tackling similar conversions.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's clarify some basic terms. A mixed number combines a whole number and a fraction, like 1 7/8. The whole number (1 in this case) represents a complete unit, while the fraction (7/8) represents a part of a unit. A fraction consists of a numerator (the top number, 7) and a denominator (the bottom number, 8). The denominator indicates the number of equal parts a unit is divided into, and the numerator shows how many of those parts are being considered.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is perhaps the most straightforward method. We first convert the fraction 7/8 into a decimal and then add the whole number 1.
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
7 ÷ 8 = 0.875
Now, we add the whole number:
1 + 0.875 = 1.875
Therefore, 1 7/8 as a decimal is 1.875.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves first converting the mixed number into an improper fraction, where the numerator is greater than or equal to the denominator. This is done by multiplying the whole number by the denominator, adding the numerator, and keeping the same denominator.
- Convert to an improper fraction:
(1 × 8) + 7 = 15
So, 1 7/8 becomes 15/8.
- Convert the improper fraction to a decimal:
15 ÷ 8 = 1.875
Again, we arrive at the same decimal equivalent: 1.875.
Method 3: Using Decimal Equivalents of Common Fractions
This method relies on memorizing the decimal equivalents of common fractions. Knowing that 1/8 = 0.125, we can easily calculate 7/8:
7/8 = 7 × (1/8) = 7 × 0.125 = 0.875
Adding the whole number 1, we get:
1 + 0.875 = 1.875
This method is efficient once you've memorized the decimal equivalents of common fractions like 1/2, 1/4, 1/8, 1/10, etc.
Understanding the Decimal Representation: Place Value
The decimal number 1.875 can be broken down into its place values:
- 1: Represents one whole unit.
- 8: Represents eight-tenths (8/10).
- 7: Represents seven-hundredths (7/100).
- 5: Represents five-thousandths (5/1000).
This illustrates the relationship between fractions and decimals – decimals are simply another way of expressing parts of a whole.
Practical Applications of Decimal Conversions
Converting fractions to decimals is vital in many real-world scenarios:
- Financial calculations: Dealing with money often involves fractions (e.g., calculating discounts, interest rates, or splitting bills).
- Measurements: Many measurements use decimal systems (e.g., centimeters, meters, inches). Converting fractional measurements to decimals is essential for accurate calculations.
- Scientific calculations: Decimals are essential in scientific computations, ensuring accuracy and ease of manipulation.
- Computer programming: Computers primarily work with decimal numbers, making fraction-to-decimal conversion crucial for programming applications.
- Engineering and construction: Precise measurements and calculations are crucial in engineering and construction, and decimals are the preferred format for these computations.
Common Misconceptions and Troubleshooting
- Incorrect division: Ensure you are dividing the numerator by the denominator correctly. Double-check your calculations to avoid errors.
- Forgetting the whole number: When dealing with mixed numbers, remember to add the whole number to the decimal equivalent of the fraction.
- Rounding errors: When rounding decimals, be mindful of the level of precision required. Rounding too early can lead to inaccuracies in calculations.
- Decimal point placement: Always pay close attention to the decimal point's position. An incorrectly placed decimal point significantly alters the value.
Frequently Asked Questions (FAQ)
- Q: Can I convert any fraction to a decimal?
A: Yes, any fraction can be converted to a decimal by dividing the numerator by the denominator. However, some fractions will result in repeating decimals (e.g., 1/3 = 0.333...).
- Q: What if the fraction has a large denominator?
A: Even with large denominators, the process remains the same: divide the numerator by the denominator. You may need a calculator for larger numbers to ensure accuracy.
- Q: How do I convert a decimal back to a fraction?
A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (e.g., 10, 100, 1000, etc.), depending on the number of decimal places. Then, simplify the fraction to its lowest terms. For example, 0.875 = 875/1000, which simplifies to 7/8.
- Q: What is the significance of using different methods?
A: Using different methods helps build a deeper understanding of the underlying concepts and provides flexibility depending on the specific fraction and the tools available. The choice of method often depends on personal preference and the context of the problem.
Conclusion
Converting 1 7/8 to its decimal equivalent, 1.875, is a straightforward process involving simple division and addition. Understanding the underlying principles of fractions and decimals is crucial for mastering this skill. By employing the different methods outlined and addressing potential misconceptions, you can confidently tackle similar conversions and appreciate the interconnectedness of these fundamental mathematical concepts. This skill is not just about numbers; it's about building a strong foundation for more advanced mathematical applications in various fields. The ability to seamlessly transition between fractions and decimals is a valuable tool that will serve you well throughout your educational journey and beyond.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 7/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.