1 3 4 To Decimal
defexpoindia
Sep 24, 2025 · 7 min read
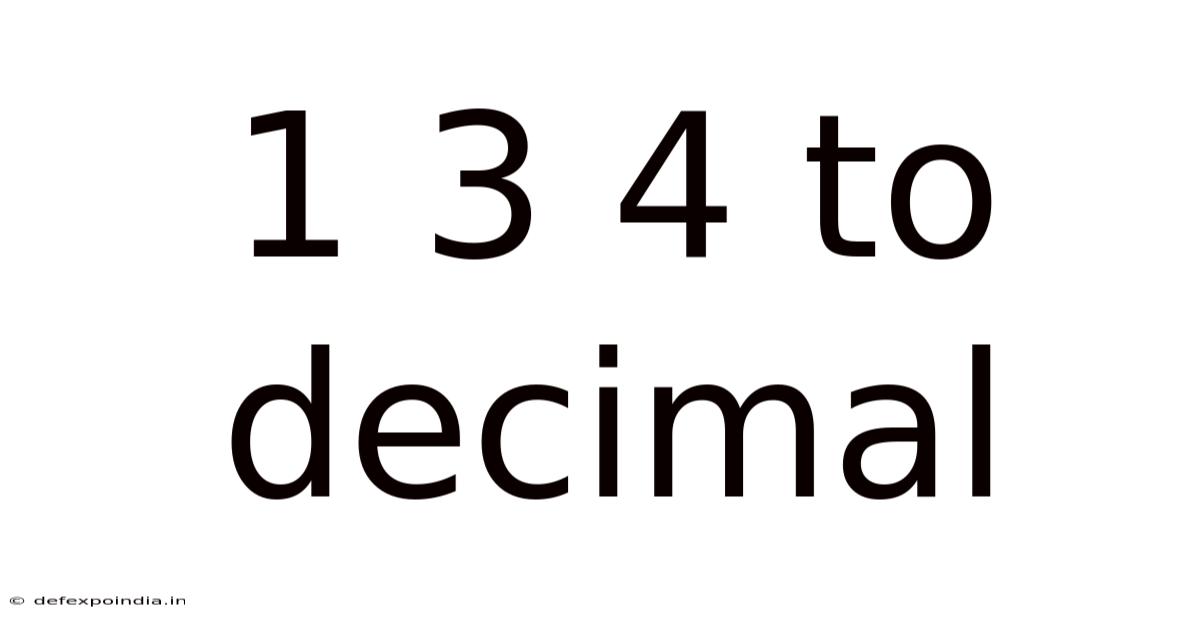
Table of Contents
Decoding the Mystery: Converting Base-4 Numbers to Decimal
Understanding different number systems is crucial in computer science, mathematics, and various other fields. While we commonly use the decimal system (base-10), other bases like binary (base-2), octal (base-8), and hexadecimal (base-16) are also prevalent. This article will delve into the process of converting numbers from base-4 to base-10 (decimal), explaining the underlying principles and providing practical examples. We'll cover various scenarios, including whole numbers, fractions, and even negative numbers, ensuring a comprehensive understanding of this essential conversion. By the end, you'll be confident in converting any base-4 number to its decimal equivalent.
Understanding Number Systems: A Quick Recap
Before diving into base-4 to decimal conversion, let's briefly review the concept of number systems. A number system is a way of representing numerical values using a specific set of symbols and rules. The base of a number system indicates the number of unique digits used.
-
Decimal (Base-10): Uses digits 0-9. Each position represents a power of 10 (10<sup>0</sup>, 10<sup>1</sup>, 10<sup>2</sup>, etc.). For example, the number 123 represents (1 x 10<sup>2</sup>) + (2 x 10<sup>1</sup>) + (3 x 10<sup>0</sup>).
-
Base-4: Uses digits 0-3. Each position represents a power of 4 (4<sup>0</sup>, 4<sup>1</sup>, 4<sup>2</sup>, etc.).
The key to converting between bases lies in understanding this positional notation. Each digit's value depends on its position relative to the radix point (the equivalent of a decimal point).
Converting Whole Numbers from Base-4 to Decimal
Converting a whole number from base-4 to decimal is a straightforward process. We simply expand the number according to its positional value and sum the results. Let's illustrate with examples:
Example 1: Converting 13<sub>4</sub> to decimal
The subscript '4' indicates the base. To convert 13<sub>4</sub> to decimal:
-
Identify the positional values: The rightmost digit is 4<sup>0</sup> (1), and the next digit to the left is 4<sup>1</sup> (4).
-
Expand the number: (1 x 4<sup>1</sup>) + (3 x 4<sup>0</sup>) = (1 x 4) + (3 x 1) = 4 + 3 = 7
Therefore, 13<sub>4</sub> = 7<sub>10</sub>
Example 2: Converting 213<sub>4</sub> to decimal
-
Identify positional values: 4<sup>0</sup> = 1, 4<sup>1</sup> = 4, 4<sup>2</sup> = 16
-
Expand the number: (2 x 4<sup>2</sup>) + (1 x 4<sup>1</sup>) + (3 x 4<sup>0</sup>) = (2 x 16) + (1 x 4) + (3 x 1) = 32 + 4 + 3 = 39
Therefore, 213<sub>4</sub> = 39<sub>10</sub>
Example 3: A Larger Number – 3210<sub>4</sub>
-
Positional values: 4<sup>0</sup> = 1, 4<sup>1</sup> = 4, 4<sup>2</sup> = 16, 4<sup>3</sup> = 64
-
Expansion: (3 x 4<sup>3</sup>) + (2 x 4<sup>2</sup>) + (1 x 4<sup>1</sup>) + (0 x 4<sup>0</sup>) = (3 x 64) + (2 x 16) + (1 x 4) + (0 x 1) = 192 + 32 + 4 + 0 = 228
Therefore, 3210<sub>4</sub> = 228<sub>10</sub>
Converting Base-4 Fractions to Decimal
Converting base-4 fractions to decimal involves a similar process, but we use negative powers of 4.
Example 1: Converting 0.3<sub>4</sub> to decimal
-
Positional values: 4<sup>-1</sup> = 0.25
-
Expansion: (3 x 4<sup>-1</sup>) = (3 x 0.25) = 0.75
Therefore, 0.3<sub>4</sub> = 0.75<sub>10</sub>
Example 2: Converting 0.13<sub>4</sub> to decimal
-
Positional values: 4<sup>-1</sup> = 0.25, 4<sup>-2</sup> = 0.0625
-
Expansion: (1 x 4<sup>-1</sup>) + (3 x 4<sup>-2</sup>) = (1 x 0.25) + (3 x 0.0625) = 0.25 + 0.1875 = 0.4375
Therefore, 0.13<sub>4</sub> = 0.4375<sub>10</sub>
Example 3: A More Complex Fractional Number – 0.213<sub>4</sub>
-
Positional values: 4<sup>-1</sup> = 0.25, 4<sup>-2</sup> = 0.0625, 4<sup>-3</sup> = 0.015625
-
Expansion: (2 x 4<sup>-1</sup>) + (1 x 4<sup>-2</sup>) + (3 x 4<sup>-3</sup>) = (2 x 0.25) + (1 x 0.0625) + (3 x 0.015625) = 0.5 + 0.0625 + 0.046875 = 0.609375
Therefore, 0.213<sub>4</sub> = 0.609375<sub>10</sub>
Converting Mixed Base-4 Numbers to Decimal
Mixed base-4 numbers (containing both whole and fractional parts) are converted by combining the methods described above.
Example: Converting 13.21<sub>4</sub> to decimal
-
Separate whole and fractional parts: 13<sub>4</sub> and 0.21<sub>4</sub>
-
Convert whole part: (1 x 4<sup>1</sup>) + (3 x 4<sup>0</sup>) = 7
-
Convert fractional part: (2 x 4<sup>-1</sup>) + (1 x 4<sup>-2</sup>) = (2 x 0.25) + (1 x 0.0625) = 0.5 + 0.0625 = 0.5625
-
Combine: 7 + 0.5625 = 7.5625
Therefore, 13.21<sub>4</sub> = 7.5625<sub>10</sub>
A Deeper Dive: The Mathematical Rationale
The process of converting from base-4 to decimal is fundamentally based on the principle of polynomial expansion. Each digit in a base-4 number represents a coefficient in a polynomial where the powers of 4 are the exponents.
For example, the number a<sub>n</sub>a<sub>n-1</sub>...a<sub>1</sub>a<sub>0</sub> in base-4 can be expressed as:
(a<sub>n</sub> x 4<sup>n</sup>) + (a<sub>n-1</sub> x 4<sup>n-1</sup>) + ... + (a<sub>1</sub> x 4<sup>1</sup>) + (a<sub>0</sub> x 4<sup>0</sup>)
This formula holds true for both whole numbers and fractional parts, with negative exponents representing the fractional portion. This mathematical foundation explains why the positional values are crucial in the conversion process.
Frequently Asked Questions (FAQ)
Q1: Can I convert negative base-4 numbers to decimal?
A1: Yes, you treat the negative sign as a separate entity. Convert the absolute value of the base-4 number to decimal and then add the negative sign back. For example, -13<sub>4</sub> would first be converted to 7<sub>10</sub> (as shown above), then become -7<sub>10</sub>.
Q2: What if a digit in the base-4 number is greater than 3?
A2: This is invalid. Base-4 only uses digits 0, 1, 2, and 3. Any digit larger than 3 indicates an error in the base-4 representation.
Q3: Are there any shortcuts for converting large base-4 numbers to decimal?
A3: While there aren't significant shortcuts, understanding the pattern of powers of 4 can help speed up the mental calculation. For instance, you might quickly recognize that 4<sup>3</sup> = 64 and 4<sup>4</sup> = 256, streamlining the expansion. Using a calculator or programming tools can efficiently handle very large numbers.
Q4: Can I convert from decimal to base-4?
A4: Absolutely! This involves a different process, primarily involving repeated division by 4 and noting the remainders. This reverse conversion is equally important and a topic worthy of further exploration.
Q5: What are the practical applications of base-4 conversions?
A5: While less common than binary or hexadecimal, base-4 has niche applications in coding theory, some specialized data representations, and certain mathematical problems. Understanding base-4 conversion enhances your overall comprehension of number systems and their manipulation.
Conclusion: Mastering Base-4 to Decimal Conversion
Converting numbers between different bases is a fundamental skill in various quantitative fields. This comprehensive guide has provided a clear and step-by-step approach to converting base-4 numbers (whole numbers, fractions, and mixed numbers) into their decimal equivalents. By grasping the underlying principles of positional notation and applying the methods explained, you can confidently tackle any base-4 to decimal conversion. Remember, practice makes perfect; the more you work through examples, the more intuitive this process will become. This newfound skill will not only boost your mathematical proficiency but also enhance your understanding of the diverse world of number systems.
Latest Posts
Latest Posts
-
How Many Volts In Amps
Sep 24, 2025
-
How Many Pounds Is 54kg
Sep 24, 2025
-
71 Square Meters To Feet
Sep 24, 2025
-
Angular Frequency To Frequency Conversion
Sep 24, 2025
-
Thwyl Mn Alansh Ala Alsntymtr
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 3 4 To Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.