1 2 Percent To Decimal
defexpoindia
Sep 21, 2025 · 5 min read
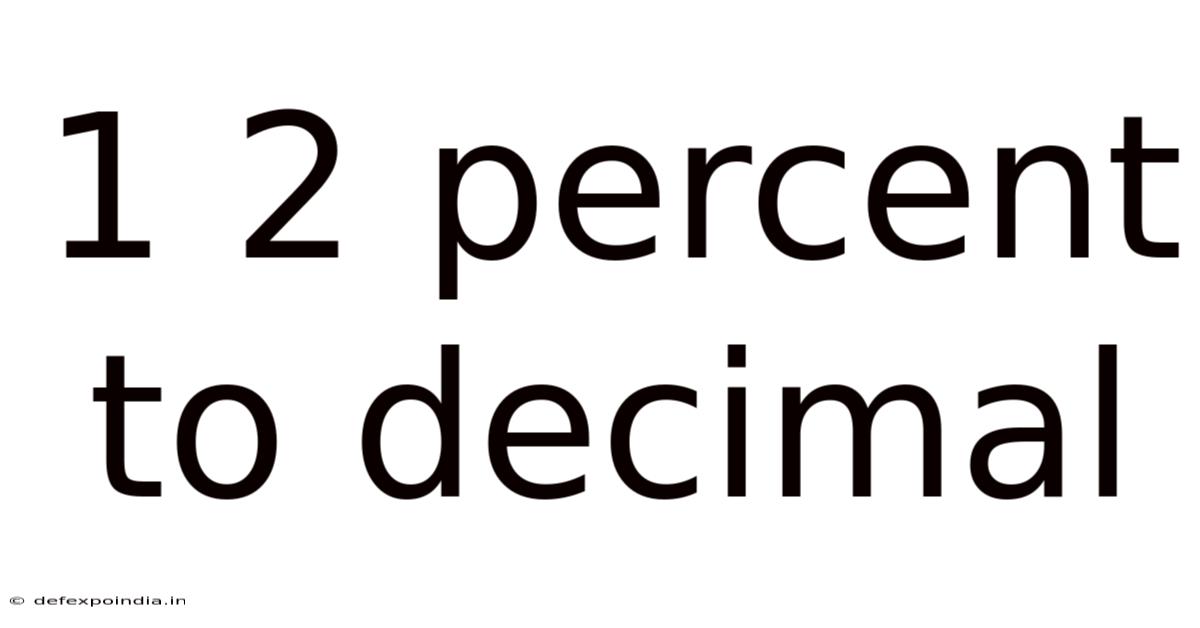
Table of Contents
Converting 1.2 Percent to Decimal: A Comprehensive Guide
Understanding how to convert percentages to decimals is a fundamental skill in mathematics and various fields like finance, statistics, and science. This comprehensive guide will walk you through the process of converting 1.2 percent to a decimal, explaining the underlying principles and providing additional examples to solidify your understanding. We'll also explore the practical applications of this conversion and address frequently asked questions. By the end, you'll be confident in converting any percentage to its decimal equivalent.
Understanding Percentages and Decimals
Before diving into the conversion, let's clarify the relationship between percentages and decimals. A percentage represents a fraction of 100. The word "percent" literally means "per hundred" ( per centum in Latin). A decimal, on the other hand, is a way of expressing a number using a base-ten system, where digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, etc.).
The key to converting percentages to decimals lies in recognizing that a percentage is simply a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, and 10% is equivalent to 10/100.
Converting 1.2 Percent to Decimal: The Step-by-Step Process
Converting 1.2% to a decimal involves a straightforward two-step process:
Step 1: Rewrite the Percentage as a Fraction
First, we write 1.2% as a fraction with a denominator of 100:
1.2% = 1.2/100
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
1.2 ÷ 100 = 0.012
Therefore, 1.2% as a decimal is 0.012.
Understanding the Logic Behind the Conversion
The conversion process is based on the fundamental relationship between percentages and decimals. Dividing by 100 effectively moves the decimal point two places to the left. This is because dividing by 100 is the same as multiplying by 1/100 or 0.01.
Let's illustrate this with another example: Converting 25% to a decimal.
25% = 25/100 = 0.25
Notice how the decimal point in 25 (which is implicitly at the end, 25.) moves two places to the left when we divide by 100, resulting in 0.25. This rule applies universally to converting any percentage to a decimal.
Practical Applications of Percentage to Decimal Conversion
The ability to convert percentages to decimals is crucial in numerous practical applications:
-
Finance: Calculating interest rates, discounts, tax rates, and investment returns often requires converting percentages to decimals. For example, calculating simple interest on a loan requires converting the interest rate (e.g., 5%) into a decimal (0.05) before applying the formula.
-
Statistics: Many statistical calculations, such as calculating probabilities, proportions, and standard deviations, involve using decimal representations of percentages.
-
Science: In scientific fields, percentages are often converted to decimals for calculations involving concentrations, ratios, and experimental data. For example, expressing the concentration of a solution as a decimal is often more convenient for calculations.
-
Everyday Life: Many everyday situations involve percentages, such as calculating tips, sales discounts, and increases or decreases in quantities. Converting these percentages to decimals simplifies the calculations involved.
More Examples of Percentage to Decimal Conversions
Let's examine a few more examples to reinforce your understanding:
- Converting 5% to a decimal: 5% = 5/100 = 0.05
- Converting 75% to a decimal: 75% = 75/100 = 0.75
- Converting 150% to a decimal: 150% = 150/100 = 1.5
- Converting 0.5% to a decimal: 0.5% = 0.5/100 = 0.005
- Converting 12.5% to a decimal: 12.5% = 12.5/100 = 0.125
Converting Decimals to Percentages: The Reverse Process
It's equally important to understand how to convert decimals back to percentages. This is simply the reverse process of what we've discussed. To convert a decimal to a percentage, you multiply the decimal by 100 and add a percent sign (%).
For example, to convert 0.25 to a percentage:
0.25 * 100 = 25%
Similarly:
- 0.05 * 100 = 5%
- 1.5 * 100 = 150%
- 0.005 * 100 = 0.5%
- 0.125 * 100 = 12.5%
Frequently Asked Questions (FAQ)
Q: What if the percentage has a fraction like 1 1/2%?
A: First, convert the mixed number to an improper fraction: 1 1/2 = 3/2. Then, express this as a fraction over 100: (3/2)/100 = 3/200. Finally, divide the numerator by the denominator: 3 ÷ 200 = 0.015.
Q: Why is it important to understand percentage to decimal conversion?
A: This conversion is fundamental for various mathematical calculations and real-world applications in fields like finance, statistics, and science. It allows for easier calculation and interpretation of data expressed as percentages.
Q: Can I use a calculator to perform this conversion?
A: Yes, most calculators have the functionality to perform this conversion directly. However, understanding the underlying principles remains essential.
Q: Are there any shortcuts for this conversion?
A: A quick shortcut is to move the decimal point two places to the left and remove the percent sign. Remember, this is a consequence of dividing by 100.
Conclusion
Converting 1.2 percent to a decimal, and more generally understanding percentage-to-decimal conversions, is a crucial skill with broad applications. By mastering this simple yet powerful conversion, you'll enhance your mathematical proficiency and improve your ability to analyze and interpret data across many disciplines. Remember the key steps: rewrite the percentage as a fraction with a denominator of 100, then divide the numerator by the denominator. Practice these steps with various examples, and you'll quickly become proficient in converting percentages to decimals and vice-versa. The ability to seamlessly switch between percentages and decimals is a valuable asset in many areas of life and study.
Latest Posts
Latest Posts
-
How Many Inches In 60cm
Sep 21, 2025
-
What Is 40in In Cm
Sep 21, 2025
-
How Long Is 8760 Hours
Sep 21, 2025
-
60 Cm Converted Into Inches
Sep 21, 2025
-
600 Meters Converted To Miles
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Percent To Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.