1 2/5 As A Percent

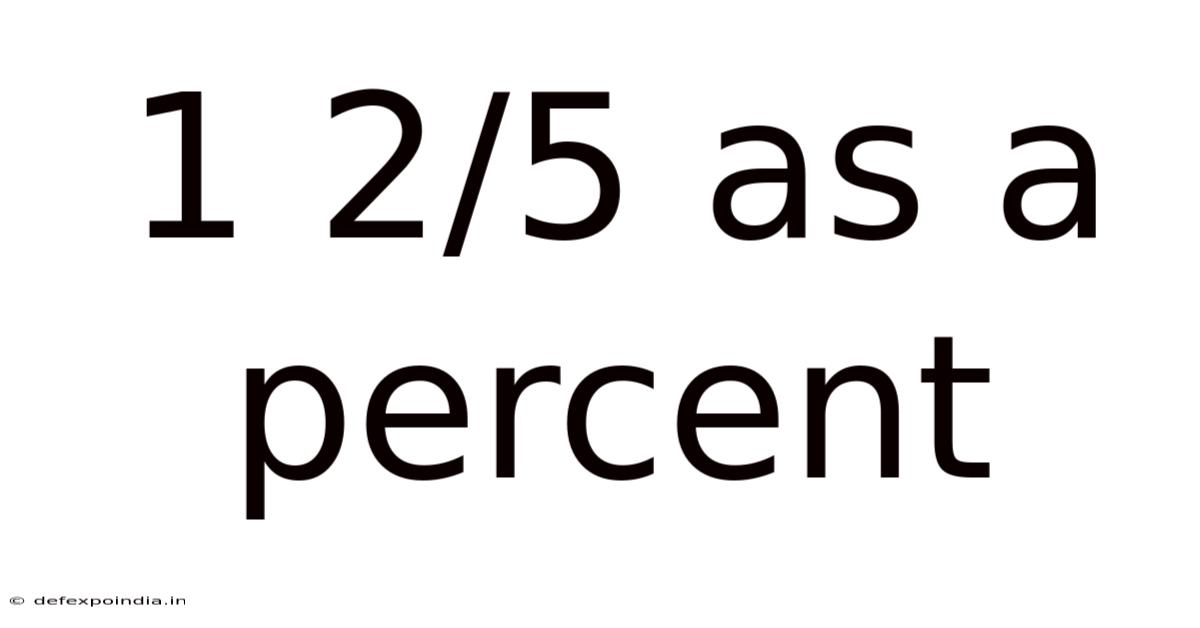
1 2/5 as a Percent: A thorough look

Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from calculating discounts in shopping to understanding statistical data. On the flip side, this thorough look will walk you through the process of converting the mixed number 1 2/5 into a percentage, explaining the underlying concepts and providing practical examples. Plus, we'll also explore different methods, ensuring you grasp the core principles and can confidently tackle similar conversions in the future. This guide will cover the fundamental concepts, step-by-step calculations, practical applications, and frequently asked questions to solidify your understanding of this important mathematical concept The details matter here. But it adds up..

Understanding the Basics: Fractions, Decimals, and Percentages

Before diving into the conversion, let's refresh our understanding of these three interconnected concepts:

Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). Here's one way to look at it: in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 parts Not complicated — just consistent. That alone is useful..
Decimals: Decimals are another way to represent parts of a whole. They use a base-10 system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. As an example, 0.5 is equivalent to 5/10 or 1/2.
Percentages: Percentages represent a fraction or decimal as a portion of 100. The symbol "%" indicates "per hundred." Here's one way to look at it: 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.

Converting 1 2/5 to a Percentage: A Step-by-Step Approach

There are several ways to convert 1 2/5 to a percentage. Let's explore two common methods:

Method 1: Converting the Mixed Number to an Improper Fraction

Convert the mixed number to an improper fraction: A mixed number combines a whole number and a fraction (e.g., 1 2/5). To convert it to an improper fraction, we multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator remains the same Most people skip this — try not to..

1 2/5 = (1 * 5 + 2) / 5 = 7/5
Convert the improper fraction to a decimal: Divide the numerator by the denominator.

7 ÷ 5 = 1.4
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percent symbol (%) And that's really what it comes down to..

1.4 * 100 = 140%

Which means, 1 2/5 is equal to 140%.

Method 2: Converting the Mixed Number Directly to a Decimal

Separate the whole number and the fraction: We can think of 1 2/5 as 1 + 2/5 It's one of those things that adds up..
Convert the fraction to a decimal: Divide the numerator (2) by the denominator (5):

2 ÷ 5 = 0.4
Add the whole number: Add the decimal equivalent of the fraction to the whole number:

1 + 0.4 = 1.4
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percent symbol:

1.4 * 100 = 140%

Again, we arrive at the answer: 1 2/5 is equal to 140%.

Understanding the Result: What Does 140% Mean?

A percentage greater than 100% signifies that the value exceeds the original whole. Think about it: in this case, 140% means that the quantity represented by 1 2/5 is 140% of the original whole, or 40% more than the original whole. This is often seen in situations of growth, increase, or surplus That's the part that actually makes a difference..

Easier said than done, but still worth knowing.

Profit Margin: A business might report a 140% profit margin, indicating a significant profit exceeding the initial investment or cost.
Growth Rate: A population might experience a 140% growth rate, exceeding its original size by 40%.
Increase in Production: A factory might increase its production by 140% exceeding its initial production level by 40%.

Practical Applications of Percentage Conversions

The ability to convert fractions and decimals to percentages is crucial in various real-world scenarios:

Calculating Discounts: If a store offers a 20% discount on an item, you can use percentage calculations to determine the final price.
Understanding Financial Statements: Financial reports use percentages extensively to express ratios, growth rates, and profit margins Which is the point..
Analyzing Statistical Data: Percentages are essential in representing and interpreting data, such as survey results or population statistics.
Calculating Taxes: Sales tax and income tax are often expressed as percentages.
Calculating Tips: Determining the appropriate tip in restaurants commonly involves percentage calculations Not complicated — just consistent. Practical, not theoretical..

Frequently Asked Questions (FAQ)

Q1: Can I convert any fraction to a percentage?

Yes, any fraction, whether proper (numerator < denominator) or improper (numerator ≥ denominator), can be converted to a percentage using the methods described above.

Q2: What if the decimal has many digits after the decimal point?

You can round the decimal to a suitable number of decimal places before converting it to a percentage depending on the desired level of precision. 4375 can be rounded to 1.To give you an idea, 1.44, resulting in 144%.

Q3: What if I have a complex fraction?

Simplify the complex fraction first into a simpler fraction (or decimal) before converting it into a percentage.

Q4: Why is 1 2/5 more than 100%?

Because 1 2/5 represents more than one whole unit. Even so, the "1" indicates one whole, and the "2/5" represents an additional fraction of a whole. The total is greater than 100% of the original whole unit Which is the point..

Q5: Are there other ways to convert fractions to percentages?

Yes, you can also use proportions to convert fractions to percentages. To give you an idea, you can set up a proportion: x/100 = 7/5 and solve for x. But this will also yield 140%. On the flip side, the methods described above are generally more straightforward and easier to understand, especially for beginners.

Conclusion

Converting fractions, decimals, and percentages is a fundamental skill with widespread applications in various fields. Day to day, by understanding the methods and practicing the conversion process, you can build a strong foundation in mathematics and confidently tackle similar problems in your studies and daily life. The conversion of 1 2/5 to 140% highlights the concept of percentages exceeding 100%, representing values greater than the original whole. Understanding the underlying concepts and mastering the conversion process is key to solving problems and interpreting data effectively. Remember that practice is key to mastering any mathematical skill, so keep practicing and exploring different problems to solidify your understanding.